Social Networking Graph

The first line of each test case contains two space-separated integers 'N' and 'E', the number of nodes and edges in the graph respectively. The following 'E' lines contain two space-separated integers 'U' and 'V', denoting an undirected edge between the nodes 'U' and 'V'. The next line contains an integer, 'M', denoting the number of queries. Then 'M' lines follow: Each line consists of two integers 'S' and 'T', where 'S' denotes the source node, and 'T' denotes the connectivity distance to be processed.

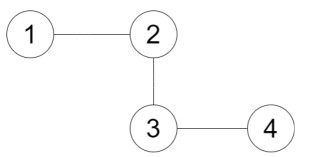
The first query asks us to find the number of nodes at a distance of 1 from node 3. Clearly, node 2 and node 4 are at a distance of 1 from node 3. Hence we get 2 as our answer. The second query asks us to find the number of nodes at a distance of 2 from node 3. Clearly, only node, i.e node 1 is at a distance of 2 from node 3. Hence we get 1 as our answer.

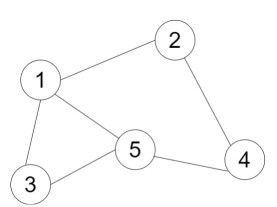
The first query asks us to find the number of nodes at a distance of 2 from node 4. Clearly, node 1 and node 4 are at a distance 2 from node 4. Hence we get 2 as our answer. The second query asks us to find the number of nodes at a distance of 1 from node 5. Clearly, node 3, node 1, and node 4 are at a distance of 1 from node 5. Hence we get 3 as our answer.

Breadth first search based approach

It’s clearly visible that we need to traverse the graph optimally in order to get our answer.We will use Breadth First Search to achieve this. Let’s understand how to do this.

We will start by making our graph. We can do this by making a unordered_map and push our nodes inside that map.
Now our graph is made and now we will head over to answer our m queries. We will start by making a socialNetwork() function, in which we will pass our source node(s), the distance connectivity(t), the number of nodes(n) and our graph.
Inside the function we will make a visited array(visited[]) of n + 1 size and assign a value of 0 to all its elements, which means they are not visited. We will also make an integer variable count(initialized to be 0), which will store our answer.
Now let’s make a queue and push our source inside and also make visited[source] = 1, which means we have visited our source.
Now we run a loop till our queue is empty. Inside this loop we will assign the value of the front of the queue to another integer variable named node and we will pop this node from the queue, and we will check if visited[node] is equal to t + 1, if this condition is met, then we increment count by 1.
Now we will run a loop to traverse all the children of this node.. And if the child has not been visited yet then push the child node into the queue, and update visited[child] = visited[node] + 1.
Once this loop is exited. Once the queue becomes empty we return count, which is our answer.
We do this for all m queries to reach our final answer.

Time Complexity

O(M * (N + E)), where ‘N’ is the number of nodes and ‘E’ is the number of edges and ‘M’ is the number of queries.

Since in the worst case, every node and every edge will be explored. Hence, N + E operations will take place. Hence for M queries it will take M*(N + E) operations. Thus, the complexity will be O(M * (N + E)).

Space Complexity

O(N + E), where ‘N’ is the number of nodes and ‘E’ is the number of edges.

Since we will be storing ‘N’ nodes and these ‘N' nodes will be connected using ‘E’ edges. Hence a total of N + E space will be used.

Problem statement

Sample Input 1:

Sample Output 1:

Explanation of Sample Input 1:

Sample Input 2:

Sample Output 2:

Explanation of Sample Input 2: