Problem

Submissions

Hints & solutions

Discuss

Square Submatrix with sum less than or equal to K

Moderate

0/80

Average time to solve is 30m

Contributed by

31 upvotes

Asked in companies

Problem statement

Given a 2-dimensional matrix of size ‘N’ x ‘M’ and an integer K. Find the size of the largest square sub-matrix whose sum is less than or equal to K. The size of a matrix is the product of rows and columns in it.

A sub-matrix is a matrix obtained from the given matrix by deletion of several (possibly, zero or all) rows/columns from the beginning and several (possibly, zero or all) rows/columns from the end. A square matrix is a matrix which has the same number of rows and columns.

For Example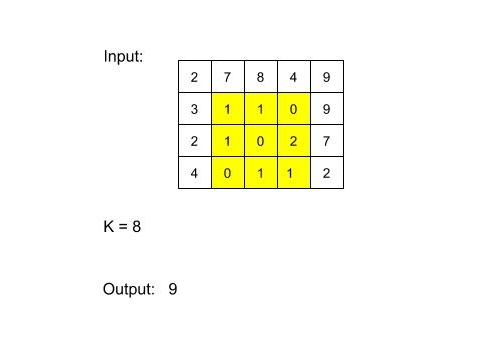

Note

If there is no square sub-matrix with a sum less than or equal to K, then return 0.

Detailed explanation ( Input/output format, Notes, Images )

Input Format

The first line of input contains an integer 'T' representing the number of test cases. Then the test cases follow.

The first line of each test case contains three single-spaced integers N, M and K, representing the number of rows, number of columns and the given integer, respectively.

The next N line contains M single-spaced elements.

Output Format

For each test case, print the size of the largest sub-matrix with sum less than or equal to K.

Print the output for each test case in a separate line.

Note

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints

1 <= T <= 10
1 <= N, M <= 100
0 <= K <= 10^5,
0 <= data <= 10^5,

where ‘data’ is the value of the elements of the matrix.

Sample Input 1

Sample Output 1

4
4
0

Explanation of Sample Input 1

In the 1st test case, there are four square submatrices of size 1(1 x 1) and one square sub-matrix of size 4(2 x 2) with sum less than or equal to K.

In the 2nd test case, the whole matrix has sum 8 which is less than 9.

In the 3rd test case, there is no square sub-matrix with sum less than or equal to K.

Sample Input 2

Sample Output 2

4
1

Hint 1

Hint 2

Hint 3

For each square sub-matrix, check if it has a sum less than or equal to K or not.

Approaches (3)

Approach 1

Approach 2

Approach 3

Brute-Force

In this approach, we will find all possible square sub-matrices and check whether it has sum less than or equal to K or not.

We will define a square sub-matrix using 3 variables (R, C, L). (R, C) denotes the top-left corner of the sub-matrix and L denotes the number of rows/column in the square sub-matrix. So, (R+L-1, C+L-1) will be the bottom-right corner of the sub-matrix.

Run a loop R from o to N-1
- Run a loop C: 0 to M-1
  - Run a loop L: 1 to Min((N-R),(M-C) )
    - Find the sum of sub-matrix (R, C, R+L-1, C+L-1)

For finding the sum of a sub-matrix, we will iterate on the elements of the sub-matrix using two loops.

Time Complexity

O((N * M)^2 * min(N, M)), where N is the number of rows and M is the number of columns in the matrix.

Considering every square sub-matrix will take O((N * M) * min(N,M)) time. In the worst case, finding the sum of a sub-matrix will take O(N * M) time. Thus, the final time complexity is O((N * M)^2 * min(N,M)).

Space Complexity

O(1)

Constant additional space is required.

(100% EXP penalty)

Square Submatrix with sum less than or equal to K

Console