Problem

Submissions

Hints & solutions

Discuss

State Diagram

Moderate

0/80

Average time to solve is 40m

Contributed by

16 upvotes

Asked in companies

Problem statement

Given a state diagram in the form of a linked list, where each node represents a unique character and has two pointers('next' and 'random'), and a string 'str', find if this string is acceptable by the state diagram or not.

The state diagram looks something like this:

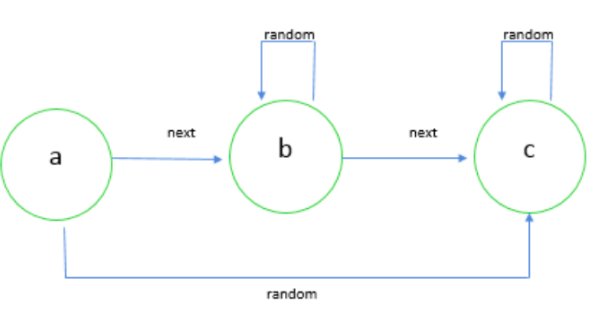
A string is said to be acceptable if and only if it matches the flow of states character by character and ends at final state i.e. state with next equal to 'null'. For the below diagram 'c' is the final state.

Note

 1. The random pointer of a node may point to NULL or to itself.
 2. All the nodes will represent unique characters.
 3. All the characters will be the lowercase alphabets.
 4. You can assume that the first state is the first character of the string.

Detailed explanation ( Input/output format, Notes, Images )

Input Format:

The first line contains a single integer 'T' that represents the number of test cases.

The first line of each test case will contain an integer ‘N’ denoting the number of states(nodes) in the state diagram.

The second line contains a string of length ‘N’ where the ith state represents the ith character of the string.

The third line contains 'N' integers a1, a2,....,an, where ai denotes the position to which the ith node’s random pointer points to. If the ith pointer points to NULL, then ai = -1.

The fourth line contains the string 'STR', which needs to be checked for the given state diagram.

Output Format:

Print “yes” in a single line if the string is acceptable by the given state diagram, “no” otherwise.

Note:

You do not need to print anything, it has already been taken care of. Just implement the given function.

Constraints:

1 < =T <= 10
1 <= N <= 26
1 <= ai <= N, or ai = -1(if pointing to NULL)
1 <= len(str) <= 10^5

Time Limit: 1 sec

Sample Input 1:

1
4
abcd
1 4 2 4
abcbddd

Sample Output 1:

yes

Explanation of the Sample Input1:

Notice that the state with character ‘b’ has its random pointer pointing to the state with the character ‘d’, and the state with the character ‘d’ (which is also the final state) has its random pointer pointing to itself.

The transitions will be as follows:

 (next)  (next) (random) (random) (random) (random)
a ----->b----->c------->b------>d ------>d ------>d(final state)

Sample Input 2:

1
3
abc
3 2 -1
abcc

Sample Output 2:

no

Hint 1

Hint 2

Implementation, try to do exactly as the problem statement says.

Approaches (2)

Approach 1

Approach 2

Recursion

This is just an implementation problem that can be easily solved using recursion.
In each iteration, we will make two calls, one to the state pointed by the next pointer, and the other to the state pointed by the random pointer of the current node,
If the character at the current state matches with the corresponding character of the string then we move forward, else we return.
If the iteration reaches the final state, and the current character of the string is its last character and it matches the character at this state, then the string is accepted by the state diagram, and we return true.

Time Complexity

O(2^N), where ‘N’ is the length of the input string.

Since we are making two recursive calls in each iteration and so, the worst-case time complexity is O(2^N).

Space Complexity

O(log(N)) where ‘N’ is the length of the string.

Since the recursion stack can grow logarithmically in the worst case depending on the length of the string and so, the total space complexity will be O(log(N)).

(100% EXP penalty)

State Diagram

Console