The Skyline Problem

Hard
0/120
Average time to solve is 15m
profile
Contributed by
8 upvotes
Asked in companies
Samsung R&D InstituteAppleUber

Problem statement

You are given 'N' rectangular buildings in a 2-dimensional city. Your task is to compute the skyline of these buildings, eliminating hidden lines return the skyline formed by these buildings collectively. A city's skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. The geometric information of each building is given in the array of buildings where BUILDINGS[i] = [LEFT_i, RIGHT_i, HEIGHT_i]:

-> LEFT_i is the x coordinate of the left edge of the ith building.

-> RIGHT_i is the x coordinate of the right edge of the ith building.

-> HEIGHT_i is the height of the ith building.

You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.

The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form [[x1, y1], [x2, y2], ...]. Each key point is the left endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark the skyline's termination where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.

Note: 
There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...,[2 3], [4 5], [7 5], [11 5], [12 7],...] is not acceptable; the three lines of height 5 should be merged into one in the final output.

As such: [..., [2 3], [4 5], [12 7],...]. 

Also, the buildings are sorted by a non-decreasing order.

For more clarification see sample case 1.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line of input contains a single integer ‘N’ denoting the number of buildings that would be given.

And the rest of the ‘N’ lines contain three space-separated integers: Left and right Indices of the vertical edges of the building while the last integer represents the height of the building ‘H’.
Output Format : 
Return the list of skylines formed by these buildings collectively.

The skyline should be represented as a list of "key points" sorted by their x-coordinate in the form [[x1, y1], [x2, y2],...]. Each key point is on the left.

The endpoint of some horizontal segment in the skyline except the last point in the list, which always has a y-coordinate 0 and is used to mark.

The skyline's termination is where the rightmost building ends. Any ground between the leftmost and rightmost buildings should be part of the skyline's contour.
Note: 
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints: 
1 <= | BUILDINGS | <= 10^4
0 <= LEFT_i < RIGHT_i <= 2^31 - 1
1 <= HEIGHT_i <= 2^31 - 1

Time Limit: 1 sec
Sample Input 1:
5
2 9 10
3 7 15
5 12 12
12 20 10
19 24 8
Sample Output 1:
2 10
3 15
7 12
12 0
15 10
20 8
24 0
Explanation for Sample 1:
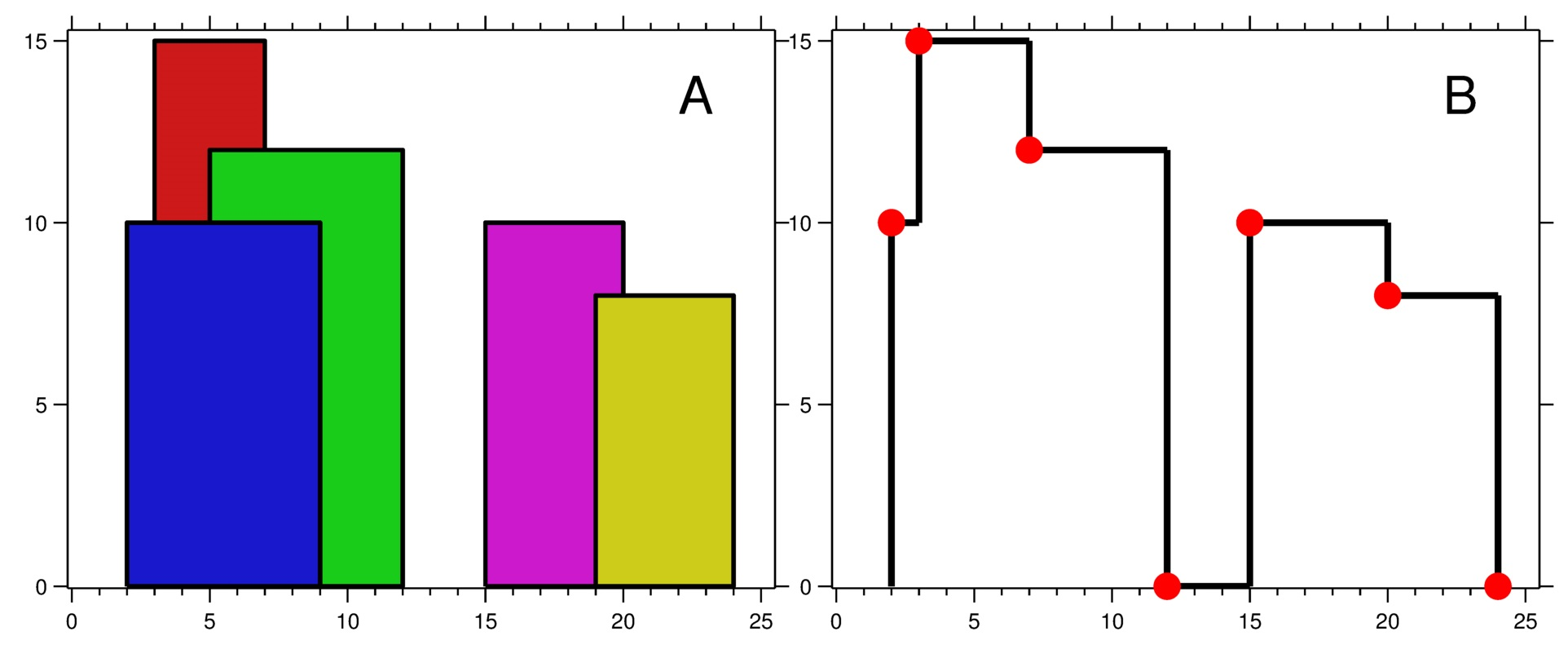
Figure A shows the buildings of the input. Figure B shows the skyline formed by those buildings. 

The red points in figure B represent the key points in the output list.

Sample Input 2:
2
0 2 3
2 5 3
Sample Output 2:
0 3
5 0
Hint

Try to sort the buildings w.r.t their heights from left to right in ascending order, store the coordinate height pair in the following manner:

(X1, X2, H) for a building would be paired up and stored in the following format:

(X1, -H), (X2, H)

Approaches (2)
Brute Force

The idea here is to first, sort the critical POINTS with respect to their coordinate and height pairs. Make a pair of 'X1' and take a negative of the height for the building so that 'X1' pairs are sorted before 'X2' pairs. Create a dictionary keeping the heights as keys and as soon as a left edge of a building is encountered, we add that building to the dictionary with its height as the key. When we encounter the right edge of a building, we remove that from the dictionary. When you hit the left edge of a building you add it to the dictionary, and when you hit the right edge of a building you delete the key. Finally, any time we encounter a critical point, after updating the dictionary we find the height of that critical point with maximum height value from keys that we already have in the dictionary to the value peeked from the top of the heap.

 

The algorithm will be-

  1. Store the coordinates and heights of the buildings paired up with each other with the first building coordinate paired after taking negative of the height and the second coordinate with positive height in a list ‘POINTS’.
  2. Now, sort edges present in the ‘POINTS’ list (array) in ascending order.
  3. The positions are now sorted from left to right, small to large. Now, initialise a dictionary named 'HEIGHTS' with zero as its first key, having a value of 1 since this would be the last height that would be added.
  4. Now, for each pair of an edge in the ‘POINTS’ list (array) and check:
    1. Update the dictionary if the current edge is a start edge (with negative height) increment the value of the key by 1.
    2. Delete the invalid buildings from the dictionary if an end edge is encountered for a key after decrementing its value by 1.
    3. Now, In each iteration update the 'SKYLINE', which records the highest building from some position, and add it to the final list of our 'SKYLINE's if the current highest is no longer the tail of the 'SKYLINE' (previous highest).
  5. We finally return the 'SKYLINE' list (array) that we have formed.
Time Complexity

O(N * N), where ‘N’ denotes the number of buildings present in the given problem.

 

Since we are finding the skylines with a custom sort on the edges and heights, therefore along with finding the maximum among the keys (heights) available in the dictionary for each iteration, So, the time complexity will be O(N * N).

Space Complexity

O(N), where ‘N’ denotes the number of buildings present in the given problem.

 

Since we are finding the skylines using a dictionary, therefore, we would require O(N) space for the problem.

Code Solution
(100% EXP penalty)
The Skyline Problem
Full screen
Console