Problem
Submissions
Hints & solutions
Discuss
Top View of the Binary Tree
Easy
0/40
Problem statement
You have been given a Binary Tree of integers. You are supposed to return the top view of the given binary tree.
Top view of the binary tree is the set of nodes which are visible when we see the tree from the top.
For example:For the given binary tree
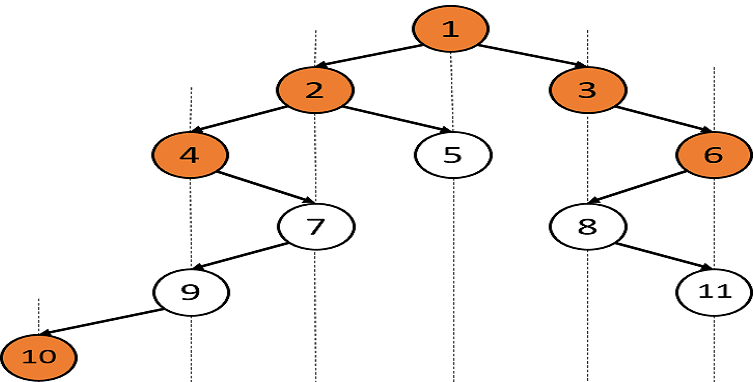
The top view of the tree will be {10, 4, 2, 1, 3, 6}.
Detailed explanation ( Input/output format, Notes, Images )
Input Format:
The first line contains an integer 'T' which denotes the number of test cases or queries to be run. Then the test cases are as follows.
The first line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.
For example, the input for the tree depicted in the below image would be :
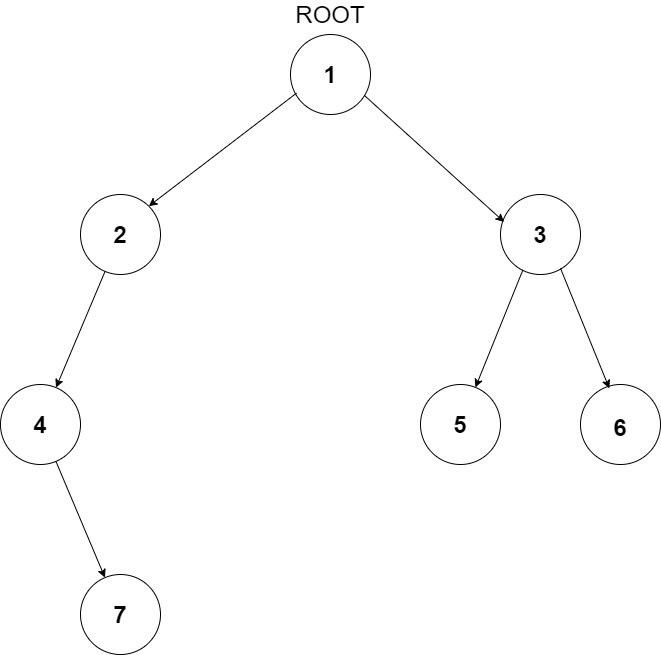
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 2
Right child of 1 = 3
Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6
Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null(-1).
The above format was just to provide clarity on how the input is formed for a given tree.
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Print all the elements of the top view of the given tree separated by a single space. And the top view nodes should be printed from left to right.
For each test case, print the output in a separate line.
You do not need to print anything; it has already been taken care of.
Constraints:
1 <= T <= 100
0 <= N <= 3000
0 <= data <= 10^6 and data != -1
Where ‘T’ is the number of test cases, and ‘N’ is the total number of nodes in the binary tree, and “data” is the value of the binary tree node.
Time Limit: 1sec
Sample Input 1:
3
1 2 3 4 5 6 7 8 9 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
1 2 3 -1 -1 -1 -1
1 3 -1 2 -1 -1 -1
Sample Output 1:
8 4 2 1 3 7
2 1 3
2 3 1
Explanation of Sample Input 1:
For the first test case,

From left to right, the top view of the tree will be {8,4,2,1,3,7}. Where 9,5 and 6 will be hidden when we see from the top of the tree.
For the second test case, from left to right, the top view of the tree will be {2,1,3}. There is nothing to hide.
For the third test case, from left to right, the top view of the tree will be {3,2,1}.
Sample Input 2:
2
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
2 7 5 2 6 -1 9 -1 -1 5 11 4 -1 -1 -1 -1 -1 -1 -1
Sample Output 2:
4 2 1 3 6
2 7 2 5 9
Explanation of Sample Input 2:
For the first test case, from left to right, the top view of the tree will be {4,2,1,3,6}. Where 7 and 5 will be hidden when we see from the top of the tree.
For the second test case, from left to right, the top view of the tree will be {2,7,2,5,9}. Where 5,6,11 and 4 will be hidden when we see from the top of the tree.
Hint
Hint 1
Hint 2
Hint 3
How will a node be hidden by another node?
Approaches (3)
Approach 1
Approach 2
Approach 3
Pre-order approach
As we know that all three traversals, i.e. pre-order, in-order and post-order, visit the tree node at once. We can use any of them. Here we are going to use pre-order traversal for the explanation. So while traversing in the pre-order traversal, we will keep track of horizontal distance of the node which is going to be visited from the root node, and we also keep track of the vertical level of that node (where the vertical level of root node would be ‘0’ and its children would be ‘1’ and so on.... ). We will be using the Map which stores the horizontal distance of the node from the root as the key and value in the map maintains a pair of containing the value of the node and the level of the node. Steps are as follows:
- Make a Map like:
- map <int, pair<int, int> > visited, where the key of “visited” defines the horizontal distance and value in the map maintains a pair of containing the value of the node and the level of the node.
- And now apply for a pre-order.
applyPreorder(root , hDistance, level,visited) = { applyPreorder(root->left , hDistance-1, level+1,visited) , applyPreorder(root->right , hDistance+1, level+1,visited )}Where ‘hDistance’ defines the horizontal distance and level defines the depth of the tree.
3. For every ‘hDistance’ check whether it is visited or not? If it is not visited, then make it visited with the value of node and “level” and if it is already visited, then check if the previous stored “level” is greater than then the current level. If yes, then store the current node because the previous node now is hidden by the current node because the current node has a lesser height.
4. Once we are done with pre-order, our map contains “hDistance” as the key and value corresponding to each “hDistance” stores the pair of nodes and their level that are visible from the top of the tree at that “hDistance”. So iterate over the map and store the value of the node in array/list. Let’s say “topView”.
5. Return the “topView”.
Time Complexity
O(N* log( N ) ), Where ‘N’ is the number of nodes in the given binary tree.
Since we are traversing at every node and storing the horizontal distance of every node into Map, So inserting an element into the map will take O(log N) time, and in the worst case (Skewed Trees) there will be ‘N’ distinct horizontal distance so it will take O(N * log(N)). While for ‘N’ element push and pop operation take O(1) time for the queue and also inserting and searching into the HashMap take O(1) time. So overall time complexity will be O(N*log(N)).
Space Complexity
O(N), Where ‘N’ is the number of nodes in the given binary tree.
We are storing the top view of the tree. So in the worst case (Skewed Trees), all nodes of the given tree will be the top view elements, so, there will be ‘N’ distinct horizontal distance to be stored and also in that case stack size for recursion will be O(N). So overall space complexity will be O(N).
Code Solution
(100% EXP penalty)
Top View of the Binary Tree
C++ (g++ 5.4)
Console



