Tree Queries

Ninja
0/200
Average time to solve is 90m
profile
Contributed by
14 upvotes
Asked in company
Rubrik, Inc.

Problem statement

You are given a tree with 'N' vertices, where each vertex has an assigned integer. You are given 'Q' queries where each query can be of two types:

1 'U' 'V': Reverse the order of all the integers on the path between 'U' and 'V'.
2 'U' 'V': Print the sum of all the integers on the path between 'U' and 'V'.
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains two space-separated integers, ‘N’ and ‘Q’, denoting the number of vertices of the tree and the number of queries.

The next N-1 lines will contain two space-separated integers u and v, denoting an undirected edge between city u and city v.

The next line contains ‘N’ space-separated integers denoting the value associated with each node.

The next q lines contain three space-separated integers representing the queries of both types.
Output Format: 
Output for each query of type two only, whether the path between the two cities of that query is alternating or not.

Output for each query will be printed in a separate line.
Note 
You are not required to print anything; it has already been taken care of. Just implement the function.
Constraints: 
1 <= N,Q <= 10^4
1 <= u,v <= N
1 <= value[i] <= 10^4

Where value[i] represents the value associated with the node.

Time Limit: 1 sec.
Sample Input 1:
12 3
1 2
2 3
3 4
1 5
5 6
5 7
1 8
8 9
9 10
9 11
9 12
10 8 5 9 12 16 8 18 21 11 19 20
2 4 7
1 1 6
2 4 7
Sample Output 1:
52
58
Explanation For Sample Output 1:

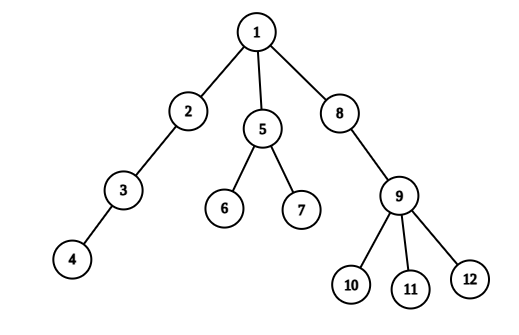
In the first query, we have to find the sum of the values of the path between node 4 and node 7. The path between 4 and 7 is 4, 3, 2, 1, 5, 7, and their corresponding height is 9, 5, 8, 10, 12, 8. 
Their sum is 52. So the output is 52.

In the second query, we have to reverse the order of the values on the path between 1 and 6. The path is 1 5 6, and their corresponding values are 10 12 16. After reversing, their values will be 16 12 10. So, the final array will be 16 8 5 9 12 10 8 18 21 11 19 20.

In the third query, we have to find the sum of the values of the path between node 4 and node 7. The path between 4 and 7 is 4, 3, 2, 1, 5, 7, and their corresponding height is 9, 5, 8, 16, 12, 8. 
Their sum is 58. So the output is 58.
Sample Input 2:
6 4
1 5
2 1
3 2
4 3
4 6
2 5 4 1 6 3
2 3 3
1 2 6
2 5 6
2 5 1
Sample Output 2:
4
21
8
Hint

Try to use heavy-light decomposition.

Approaches (1)
Heavy-light Decomposition

We will use heavy-light decomposition to solve this problem. The idea of this algorithm is that we will try to break the given tree into some segments where we can apply the segment tree to process each query in logarithmic time. 
 

Algorithm: 

 

  • update function:
    • It takes a node as an argument and updates the size and the sum of the node.
  • propagate function:
    • It is a recursive function that takes a node as an argument and reverses the order of the values in the subtree.
  • merge function:
    • It merges the left subtree and right subtree into the root node.
  • split function:
    • It splits a node into the child nodes and updates the information of the current node.
  • dfs function:
    • It traverses the tree and calculates the depth, parent, and subtree size of each node.
  • hld function:
    • It breaks the tree into different segments(chains) and calculates the chain number and head of the chain for each node.
  • lca function:
    • It takes two nodes as an argument and returns the lower node among them when they are lifted and comes in the same chain.
  • getLastChainInd function:
    • It takes two nodes as an argument and returns the index of the chain, which contains both the node when lifted upward.
  • queryUp function:
    • It takes two nodes as an argument and returns the sum of all the values on the path between them.
  • queryPath:
    • It returns the sum of all the values on the path between two nodes with the help of the queryUp function.
  • splitUp function:
    • It splits the path between two given nodes and reverses the path between them.
  • mergeUp function:
    • It merges the path between two given nodes, maintaining the order of the path.
  • reversePath function:
    • It takes two nodes as an argument and reverses the order of the values on the path between them.
  • given function:
    • Represent the tree in adjacency array.
    • Call the above functions for pre-processing.
    • Iterate over all the queries.
      • If it is of the first type, reverse the order of the path.
      • Else calculate the sum of all the values on the path between the two nodes.
Time Complexity

O( Q * (log(N))^2 ), where ‘Q’ is the number of queries and ‘N’ is the number of nodes.

 

Since we are iterating the ‘Q’ queries and in each query, we are querying the heavy segments(chains) and the maximum number of heavy segments(chains) can be log(N). So the overall time complexity will be O( Q * (log(N))^2 ).

Space Complexity

O(N), where ‘N’ is the number of nodes.

 

The space required by all the auxiliary array is of order O(N).

Code Solution
(100% EXP penalty)
Tree Queries
Full screen
Console