Two cliques

Moderate
0/80
Average time to solve is 10m
profile
Contributed by
12 upvotes
Asked in companies
BarclaysCadence Design Systems

Problem statement

You are given an undirected graph of ‘N’ nodes and ‘M’ edges. Your task is to print 1 if this graph can be divided into exactly two disjoint cliques. Else, you need to print 0.

Note : 
Let G be a subgraph of the given graph. Then, G is said to be a clique if G is a complete graph.

Two cliques are said to be disjoint if they don’t have a common node.
Detailed explanation ( Input/output format, Notes, Images )
Input Format : 
The first line of input contains an integer 'T' representing the number of test cases.

The first line of each test case contains two space-separated integers ‘N’ and ‘M’. Here ‘N’ denotes the total number of nodes and ‘M’ denotes the total number of edges in the graph.

The next ‘M’ lines contain two space-separated integers ‘U’ and ‘V’. Here ‘U’ and ‘V’ represent the nodes that share an edge.
Output Format : 
For each test case, print 1 if the given graph can be divided into exactly two disjoint cliques, else print 0.

The output of each test case will be printed in a separate line.
Note : 
 You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints : 
1 <= T <= 5
1 <= N <= 100
1 <= M <= N * (N - 1) / 2
0 <= U, V <= N - 1
Sample Input 1 :
2
4 2
0 1
2 3
5 4
0 1
0 2
0 3
2 4
Sample Output 1 :
1
0
Explanation For Sample Input 1 :
Test Case 1 :  
The given graph is shown below.

1 

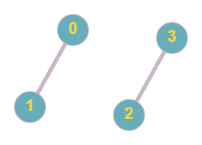
The above graph can be divided into two disjoint cliques {0, 1} and {2, 3}. 

Test Case 2 : 
The given graph is shown below.

2

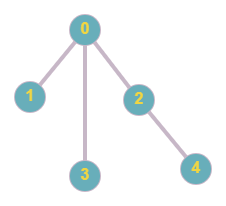
The above graph cannot be divided into two disjoint cliques.
Sample Input 2 :
2
6 7
0 1
0 2
1 2
3 2
3 4
3 5
4 5
5 4 
0 1
0 4
1 2
2 3
Sample Output 2 :
1
0
Hint

Take complement of the graph and try to find a solution using properties of the bipartite graph.

Approaches (1)
Bipartite graph Approach

The idea here is first to take a complement of the graph. Then the problem reduces to check if the given graph is a bipartite graph or not. Because bipartite is a graph that can be divided into two sets such that no two nodes of the same set have a common edge it means in the original graph every two nodes of the same set are completely connected i.e. the set will be a complete graph.   

 

To check whether a graph is bipartite or not we will color the graph using 2 colors such that adjacent elements will have different colors. If we are not able to do such coloring then it shows that the bipartite graph is not possible.

 

Algorithm:

 

  • Declare the following things:
  • A 2-D array to store the adjacency matrix of the graph, say ‘adj’.
  • A color array to keep track of colors of the nodes and initialize all elements of the color array with -1.
  • Build an adjacency matrix of complement graph using the given edge list.
  • Run a loop from i = 0 to ‘N’. Here, ‘N’ is the total number of nodes in the given graph.
  • Check if the subgraph starting at node ‘i’ is a bipartite graph or not, by calling the ‘isBipartite’ function. If the ‘isBipartite’ function returns false then return false.
  • Return true as the given graph is a bipartite graph.

 

 Description of isBipartite function : 

 

This function is used to check whether the subgraph starting from vertex ‘u’ is a bipartite graph or not.

 

This function will take 3 arguments 

 

  • A variable ‘u’ denoting the starting node.
  • An array ‘color’ to keep track of colors of nodes of the graph.
  • A 2 – D array ‘adj’ denotes the adjacency matrix of the graph.

bool isBipartite(u, color, adj) : 

  • Assign ‘u’ as color = 0.
  • Declare an empty queue say, ‘q’, and push ‘u’ to it.
  • Run a loop until ‘q’ is not empty:
  • Pop front node from ‘q’ say, ‘current’.
  • Visit all neighbours of the ‘current’ node:
  • Say current neighbor of ‘current’ is v.
  • If the color of v equals -1 then assign color equals to (color[current] ^ 1 )  as we need to assign different colors to adjacent nodes. Also push v into the queue.
  • Else if ‘color[current]’ equals to ‘color[v]’ then return false as two–coloring is not possible in this subgraph and hence the given graph is not a bipartite graph.
  • Return true as we have colored all adjacent nodes in different colors.
Time Complexity

O(N ^ 2), where ‘N’ is the total number of nodes in the graph.

 

Building an adjacency matrix of graph takes O(N ^ 2) time. Also, checking whether the graph is a bipartite or not takes O(N) time as we need to visit O(N) nodes in the worst case.

Hence, the overall time complexity will be O(N ^ 2) + O(N) = O(N ^ 2).

Space Complexity

O(N ^ 2), where ‘N’ is the total number of nodes in the graph.

 

We are using a distance color that takes O(N) space. Also, we are using a queue that takes O(N) space as there can be O(N) nodes in the queue in the worst case. Also, we are using an Adjacency matrix that takes O(N ^ 2) space.


Hence, the overall space complexity will be O(N) + O(N)  + O(N ^ 2) = O(N ^ 2).

Code Solution
(100% EXP penalty)
Two cliques
Full screen
Console