Two Stacks

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
249 upvotes
Asked in companies
MicrosoftVisa

Problem statement

Design a data structure, which represents two stacks using only one array common for both stacks. The data structure should support the following operations:

push1(NUM) - Push ‘NUM’ into stack1.
push2(NUM) - Push ‘NUM’ into stack2.
pop1() - Pop out a top element from stack1 and return popped element, in case of underflow return -1.
pop2() - Pop out a top element from stack2 and return popped element, in case of underflow return -1.

There are 2 types of queries in the input

Type 1 - These queries correspond to Push operation.
Type 2 - These queries correspond to Pop operation.

Note:

1. You are given the size of the array.

2. You need to perform push and pop operations in such a way that we are able to push elements in the stack until there is some empty space available in the array.

3. While performing Push operations, do nothing in the situation of the overflow of the stack.
Detailed explanation ( Input/output format, Notes, Images )
Input format: 
The first line of the input contains two space-separated integers 'S' and 'Q', denoting the size of the array and number of operations to be performed respectively.

The next 'Q' lines contain operations, one per line. Each line begins with two integers ‘type’ and ‘stackNo’, denoting the type of query as mentioned above and the stack number on which this operation is going to be performed.

If the ‘type’ is 1 then it will be followed by one more integer ‘NUM’ denoting the element needed to be pushed to stack ‘stackNo’.
Output format: 
For each operation of Type 2, print an integer on a single line - popped element from the stack, if the stack is already empty print -1.
Note: 
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
0 <= S <= 10^5
1 <= Q <= 5*10^5
1 <= type, stackNo <= 2
0 <= NUM <= 10^9

Time Limit: 1 sec.
Sample Input 1:
3 5
1 1 3
1 2 4
1 1 5
2 1
2 2
Sample output 1:
5
4
Explanation of sample input 1:

alt-text

Here every step shows a snapshot of 2 stacks after each operation.

Initialising the size of the array to 3, twoStack = new TwoStack(3).
Then operation on two stacks occurs as follows:
twoStack.push1(3) // pushing 3 in stack1.
twoStack.push2(4) // pushing 4 in stack2.
twoStack.push1(5) // pushing 5 in stack1.
twoStack.pop1() // popping out from stack2, it returns 5.
twoStack.pop2() // popping out from stack2, it returns 4.
Sample Input 2:
3 10
1 1 2
1 1 4
1 1 3
1 2 5
2 2
2 1
1 2 6
2 2
2 1
1 2 7
Sample output 2:
-1
3
6
4
Explanation of sample input 2:

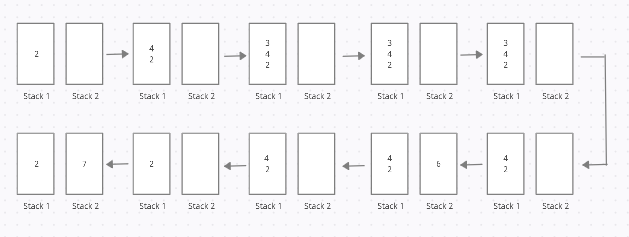
alt-text

Here every step shows a snapshot of 2 stacks after each operation.

Initialising the size of the array to 3, twoStack = new TwoStack(3).
Then operation on two stacks occurs as follows:
twoStack.push1(2) // pushing 2 in stack1.
twoStack.push1(4) // pushing 4 in stack1.
twoStack.push1(3) // pushing 3 in stack1.
twoStack.push2(5) // pushing 5 in stack2, but 3 elements are already in the array and there is no empty space hence it cannot be added.
twoStack.pop2() // popping out from stack2, it is already empty hence returns -1.
twoStack.pop1() // popping out from stack1, it returns 3.
twoStack.push2(6) // pushing 6 in stack2.
twoStack.pop2() // popping out from stack2, it returns 6.
twoStack.pop1() // popping out from stack1, it returns 4.
twoStack.push2(7) // pushing 7 in stack2.
Hint

Start top of the two stacks from the two extremes of the array.

Approaches (1)
Optimal solution
  • To utilise the array space optimally, we start the top of both stacks from the extreme of the array.
    • Let the array used by both the stacks is Arr, having size equals to ‘s’.
    • Let’s say top1 and top2 points to the top of the stacks, stack1 and stack2 respectively.
    • As the size of the array is ‘s’, we assign -1 to top1 and  ‘s’ to top2 (keeping 0 based indexing in mind) which denotes both stacks are currently empty.
  • In order to complete push operations (or operation of Type 1) we do as follows:
    • push1(num):
      • Check if Arr has enough space to push an integer or not. For this, we check top1 + 1 < top2, if this is the case then we have enough space then, we increment top1 by 1 and assign num to Arr[top1].
      • If there is insufficient space for pushing another element, which will happen in case top1 + 1 == top2. So we do nothing and just return.
    • push2(num):
      • Check if Arr has enough space to push an integer or not. For this we check top2 - 1 > top1, if this is the case then we have enough space then, we decrement top2 by 1 and assign num to Arr[top2].
      • If there is insufficient space for pushing another element, which will happen in case top2 - 1 == top1. So we do nothing and just return.
  • In order to complete pop operations (or operations of Type 2) we do as follows:
    • pop1():
      • First, we check if the stack1 is empty or not, for which we just need to check if top1 is -1 or not, it is equal to -1 then it is the condition of underflow, so we just return -1.
      • If stack1 is not empty, then we decrement top1 by 1 and return the value of Arr[top1+1].
    • pop2():
      • First, we check if the stack2 is empty or not, for which we just need to check if top2 is equal to 's' or not, it is equal to ‘s’ then, it is the condition of underflow, so we just return -1.
      • If stack2 is not empty, then we increment top2 by 1 and return the value of Arr[top2-1].
  • This way we can utilise the total empty space of the array available at any instant of time.
Time Complexity

O(1) for push operation, as it only takes constant time to push an element into the stack.

 

O(1) for pop operation, as it only takes constant time to pop out an element out of the stack.

Space Complexity

O(N), where N is the size of the array used for two stack's implementation.

 

As we need to store stack values in the array and at some instant of time sizes of two stacks can be N.

Code Solution
(100% EXP penalty)
Two Stacks
Full screen
Console