Problem

Submissions

Hints & solutions

Discuss

Two Sum IV - Input is a BST

Moderate

0/80

Average time to solve is 30m

Contributed by

54 upvotes

Asked in companies

Problem statement

You have been given a Binary Search Tree and a target value. You need to find out whether there exists a pair of node values in the BST, such that their sum is equal to the target value.

A binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree whose internal nodes each store a value greater than all the values keys in the node's left subtree and less than those in its right subtree.

Follow Up:

Can you solve this in O(N) time, and O(H) space complexity?

Detailed explanation ( Input/output format, Notes, Images )

Input format:

The first line of input contains a single integer T, representing the number of test cases or queries to be run. 

Then the T test cases follow. 

The first line of each test case contains elements in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place. 

The second line of each test case contains a single integer representing the target value.

For example, the input for the tree depicted in the below image would be :

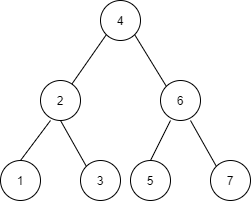
4 2 6 1 3 5 7 -1 -1 -1 -1 -1 -1 -1 -1

Explanation :

Level 1 :
The root node of the tree is 4

Level 2 :
Left child of 4 = 2
Right child of 4 = 6

Level 3 :
Left child of 2 = 1
Right child of 2 = 3
Left child of 6 = 5
Right child of 6 = 7

Level 4 :
Left child of 1 = null (-1)
Right child of 1 = null (-1)
Left child of 3 = null (-1)
Right child of 3 = null (-1)
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).

Note :

The above format was just to provide clarity on how the input is formed for a given tree. 
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:    
4 2 6 1 3 5 7 -1 -1 -1 -1 -1 -1 -1 -1

Output format:

For each test case, print True or False in a separate line.

Note:

You do not need to print anything. It has already been taken care of. Just implement the given function.

Constraints:

1 <= T <= 100
1 <= N <= 3000
-10^9 <= node data <= 10^9, (where node data != -1)
-10^9 <= target value <= 10^9

Where N denotes is the number of nodes in the given tree.

Time Limit: 1 second

Sample Input 1:

1
10 6 12 2 8 11 15 -1 -1 -1 -1 -1 -1 -1 -1
14

Sample Output 1:

True

Explanation for sample 1:

For the first test case, the sum of the nodes with values 2 and 12 equals the target value.

Sample Input 2:

1
5 3 7 -1 -1 6 8 -1 -1 -1 -1
20

Sample output 2:

False

Explanation for sample 2:

For the first test case, there is no such pair of nodes, the sum of which equals the target value.

Hint 1

Hint 2

Hint 3

Hint 4

Think of a brute-force solution to search a node with target-node value by using the property of BST.

Approaches (4)

Approach 1

Approach 2

Approach 3

Approach 4

Brute-force

The idea is to traverse the BST in a level-order manner and let’s denote the value of the current node as A. For each node, check whether the node with value (target - A) is present in the BST or not. We can search this node in the given tree using the BST property, i.e. at any node we go to left subtree or right subtree by comparing the node value to (target - A), and if the value is found in the BST, return true. If the value is not found for any node, return false.

Time Complexity

O(N*H), where N is the number of nodes, and H is the height of the given BST(Binary Search Tree).

In the worst case, we will be traversing each node of BST O(N), and for each node, we are searching in a given BST which can take O(H) time. Hence, the overall time complexity will be O(N*H).

Space Complexity

O(N), where N is the total number of nodes in the given BST.

In the worst case, almost all the nodes of the tree will be pushed into the queue, and extra space will be required for recursion stack. Hence, the overall space complexity will be O(N).

(100% EXP penalty)

Two Sum IV - Input is a BST

Console