Upside Down Binary Tree

Moderate
0/80
Average time to solve is 15m
profile
Contributed by
9 upvotes
Asked in company
Barclays

Problem statement

You are given a rooted binary tree. In this binary tree, all the right nodes are either a leaf node with a sibling (left node sharing the same parent node) or empty. Your task is to flip this tree upside down such that all right nodes turn into left leaf nodes.

You are given the 'ROOT' of the binary tree. Your task is to return the new 'ROOT' after turning the tree upside down.

For Example: 
Tree = [5, 4, 3, 1, 2, -1, -1, -1, -1, -1, -1]

sample_image

 Upside down Tree :

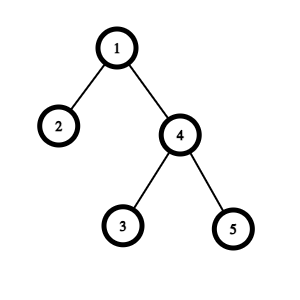
sample_output

ANS = [1, 2, 4, -1, -1, 3, 5, -1, -1, -1, -1]
Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains an Integer 'T' which denotes the number of test cases or queries to be run. Then the test cases follow.

The first line of each test case contains the elements of the tree in the level order form separated by a single space.

If any node does not have a left or right child, take -1 in its place. Refer to the samples below.
Output Format: 
For each test case, output the upside-down binary tree. 
Output for each test case will be printed in a separate line.
Note: 
You don’t need to print anything. It has already been taken care of. Just implement the given function.
Constraints: 
1 <= T <= 100
1 <= N <= 5000 
1 <= node.values <= 10 ^ 9

Time Limit: 1 second
Sample Input 1:
2
1 6 7 -1 -1 -1 -1 
6 9 10 4 13 -1 -1 -1 -1 -1 -1
Sample Output 1:
6 7 1 -1 -1 -1 -1
4 13 9 -1 -1 10 6 -1 -1 -1 -1
Explanation For Sample Output 1:
For the first test case:

Original tree:

alt

After turning upside down:

alt

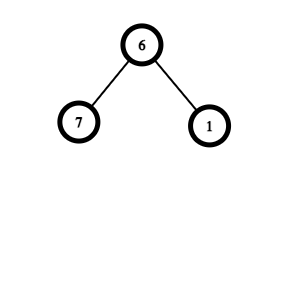
For second test case:

Orignal Tree:

alt

After turning upside down:

alt

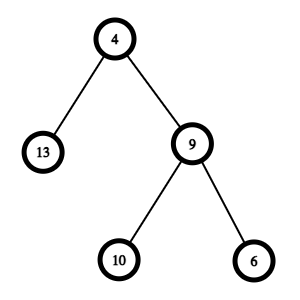
Sample Input 2:
2
10 -1 -1 
1 2 3 4 5 -1 -1 6 7 -1 -1 -1 -1 -1 -1
Sample Output 2:
10 -1 -1
6 7 4 -1 -1 5 2 -1 -1 3 1 -1 -1 -1 -1
Hint

Can we solve this problem recursively? Every time going to the left child?

Approaches (1)
Recursive Approach

We will first recursively solve the left subtree and then, recursion will return the rightmost node of the upside-down tree of the left subtree, then we will add the right child of the current node to the left of the returned rightmost node. And the current node to the right of the returned node. 

 

After this current node becomes the rightmost node of the upside-down tree and we will return it. The new root node will be the left-most node in the given tree and we will return it in the recursion.

 

The algorithm will be:

 

  1. recursiveTraversal (node):
    1. If (node.left == NULL)
      1. return node, node
    2. rightMostChild, ans = recursiveTraversal(node.left)
    3. rightMostChild.left = node.right
    4. rightMostChild.right = node
    5. node.left = None
    6. Node.right = None
    7. return node, ans
  2. upsideDownTree(root) :
    1. node , ans =  recursiveTraversal(root)
    2. return ans
Time Complexity

    O(N), where ‘N’ is the number of nodes in the tree. 

 

    We are visiting each node exactly once. 

Space Complexity

    O(N), where ‘N’ is the number of nodes in the tree. 

 

   Since O(N) space is required for recursion call stack

Code Solution
(100% EXP penalty)
Upside Down Binary Tree
Full screen
Console