Zero Matrix

Easy
0/40
Average time to solve is 20m
profile
Contributed by
382 upvotes
Asked in companies
Goldman SachsAmazonRedBus

Problem statement

You are given a matrix 'MATRIX' of dimension 'N' x 'M'. Your task is to make all the elements of row 'i' and column 'j' equal to 0 if any element in the ith row or jth column of the matrix is 0.

Note:

1) The number of rows should be at least 1.

2) The number of columns should be at least 1.

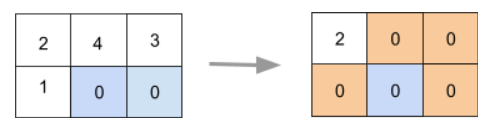
3) For example, refer to the below matrix illustration:

altImage

Detailed explanation ( Input/output format, Notes, Images )
Input Format: 
The first line contains two space-separated integers, 'N' and 'M', as described in the problem statement.

The next 'N' lines contain 'M' integers separated by spaces describing rows of the matrix.
Output Format: 
Return 'N' rows consisting of 'M' integers representing the matrix.
Note: 
You don't need to print anything, it has already been taken care of. Just implement the given function.
Constraints: 
1 <= N <= 100
1 <= M <= 100
-10^9 <= MATRIX[i][j] <= 10^9

Where 'MATRIX[i][j]' denotes the matrix element.

Follow Up:

Can you solve it with the space complexity of O(1)?

Time limit: 1 sec


Sample Input 1:
2 3
2 4 3
1 0 0
Sample Output 1:
2 0 0 
0 0 0
Sample Input 2:
1 1 
5
Sample Output 2:
5


Hints:

1. Think about how to identify the rows and columns containing a '0' element and then modify the matrix accordingly to make all elements in those rows and columns equal to 0.
2. You can use the first row and first column of the matrix itself as indicators to mark whether a particular row or column needs to be zeroed
Approaches (2)
Extra vector for row and column

We can use two vectors of datatype bool of size ‘N’ and ‘M’, let say ‘ROW’ and 'COL' respectively.

 

The steps are as follows:

 

  • Initialize both the vectors with the false.
  • We are aiming to change the entry of the vector from false to true if we found any element which is 0 in that row for the ‘ROW’ vector and column for the 'COL' vector.
  • Run a loop to N times for the ‘ROW’, in each iteration:
    • Run a loop to M times for the entries in that ‘ROW’, in each iteration:
      • If ‘MATRIX[i][j]' is 0, then mark ‘ROW[i]' = true and ‘COL[j]’ = true because we have to set entire ith row and entire jth column of the matrix ‘MATRIX’ to 0, where 0 <= ‘i’ < ‘N’ and 0 <= ‘j’ < ‘M’ and ‘i’ is for row and ‘j’ is for column.
  • After the completion of the above steps, the ‘ROW’ vector contains true for those for which we have to set the entire row 0, and the 'COL' vector contains true for those for which we have to set the entire column 0.
  • Again, run a loop to ‘N’ times for the ‘ROW’, in each iteration:
    • Run a loop to ‘M’ times for the entries in that ‘ROW’, in each iteration:
      • If ‘ROW’[i]' = true or ‘COL[j]’ = true, then set ‘MATRIX[i][j]' = 0.
      • Else, leave ‘MATRIX[i][j]' as it is.
  • Finally, return the matrix ‘MATRIX’.
Time Complexity

O(N*M), Where ‘N’ is the number of rows and ‘M’ is the number of columns.

 

Since we are traversing the whole matrix of size N * M. Thus the time complexity will be O(N * M).

Space Complexity

O(N + M), Where ‘N’ is the number of rows and ‘M’ is the number of columns.

 

Since we are creating two vectors of the size ‘N’ and ‘M’ for the row and column respectively. Thus the space complexity will be O(N + M).

Code Solution
(100% EXP penalty)
Zero Matrix
Full screen
Console