Problem

Submissions

Hints & solutions

Discuss

Count unique BSTs.

Hard

0/120

Average time to solve is 15m

Contributed by

18 upvotes

Asked in company

Problem statement

You have been given a number ‘NUM’. Your task is to count total structurally unique binary search trees from keys 1 to ‘NUM’ considering we should use each key from 1 to ‘NUM’ only once.

Two binary search trees are different if there is at least one node during traversal which is different in values or present in one tree but not present in another tree.

Note:

The answer can be large, hence the return answer % ‘MOD’, where ‘MOD’ is a large prime number (10^9 + 7).

Detailed explanation ( Input/output format, Notes, Images )

Input format :

The first line contains a single integer ‘T’ representing the number of test cases.

The first line of each test case will contain a single integer ‘NUM’ where ‘NUM’ represents the number of keys.

Output Format :

For each test case, print a single line containing the count of total structurally unique binary search trees.

The output of each test case will be printed in a separate line.

Note:

You don’t need to print anything; It has already been taken care of. Just implement the given function.

Constraints:

1 <= T <= 100   
1 <= NUM <= 500

Time limit: 1 sec

Sample Input 1:

2
2
1

Sample Output 1:

2
1

Explanation of sample input 1:

In the first test case, 2 unique BST are possible.

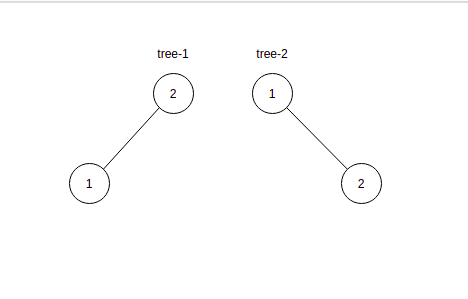
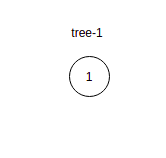
In the second test case, only 1 tree is possible.

Sample Input 2:

2
3
4

Sample Output 2:

5
14

Explanation of sample input 2:

In the first test case, 5 unique BST are possible.

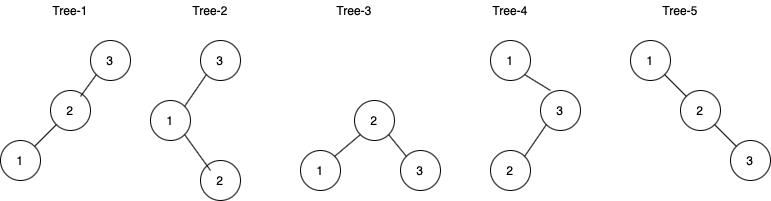
In the second test case, similar to the above way, 14 unique BST are possible.

Hint 1

Hint 2

Hint 3

Can you solve the problem recursively?

Approaches (3)

Approach 1

Approach 2

Approach 3

Recursion

We can assume a function for calculating the number of ways to calculate the number of trees for the given number of nodes for a fixed root. So we could calculate the number of ways to make a tree as follows. Let’s call the function F(‘X’) giving the number of trees given ‘X’ number of nodes.

We could calculate F(‘X’) = sum of { F(‘i’) * F(‘X’-1-’i’) }. Where i is the assumed number of nodes in the left child of the current root and so the number of remaining nodes for the right child is equal to (‘X’-1-i), hence we could add all these ways multiplicatively, so we could get the total number of ways.

This value of this function is also defined as Catalan number, which has a specified formula which is equal to ((2*NUM) C (NUM) / (NUM+1)) , but we will calculate the value recursively.

Steps for calculating assuming ‘NUM’ number of nodes in the given tree are as follows:

If ‘NUM’ is equal to 0 or 1, return the answer as 1, as there is only one tree.
Declare variable ‘SUM’ and initialize it with 0, where sum will store the count of total structurally unique binary search trees.
Run a loop for ‘i’ = ‘0’ to ‘NUM’-1:
1. ‘SUM’ = ‘SUM’ + F(‘i’) * F(‘NUM’-1-’i’) to the answer.
Finally, return ‘SUM’ as the answer.

Time Complexity

O(3 ^ NUM), where ‘NUM’ is the number of distinct keys.

The complexity estimation for above recursion can be done as follows:

Let's call the estimation function T(‘NUM’) for ‘NUM’ number of nodes , here it represents the number of recursive calls for ‘NUM’.

A call for N takes exactly 2 * (NUM - 1) recursive calls, each of them adding their own costs , 2 * ( T(1) + T(2) + … + T(NUM-1)).
A call for N + 1 takes exactly 2 * N recursive calls. Each of them adding their own cost, 2 * ( T(1) + T(2) + … + T(NUM-1) + T(NUM)).
T(NUM+1) - T(NUM) = 2 + 2 * T(NUM)
T(NUM) = 3 * T (NUM-1) + 2
T(NUM) = 3 ^ NUM

And hence time complexity will be O(3 ^ NUM).

Space Complexity

O(3 ^ NUM), where ‘NUM’ is the number of distinct keys.

We can follow the same runtime complexity estimation as we are also creating the same amount of variables in the recursion stack memory and hence space complexity will be O(3 ^ NUM).

(100% EXP penalty)

Count unique BSTs.

Pradeep Suryavanshi

Interview problems

C++ Easy Solution

const int MOD = 1000000007;

long long totalTrees(int num){

vector<long long> dp(num + 1, 0);

dp[0] = 1;

dp[1] = 1;

for (int i = 2; i <= num; ++i) {

for (int j = 1; j <= i; ++j) {

dp[i] = (dp[i] + dp[j-1] * dp[i-j]) % MOD;

}

return dp[num];

}

41 views

0 replies

0 upvotes

Raushan Kumar

Interview problems

C++ DP Solution

long long int mod = 1e9+7;

long long solveRec(int n)

{

if(n<=1)

return 1;

long long ans = 0;

// think i as root node

for(int i=1; i<=n; i++) {

ans = ( ans + (solveRec(i-1) * solveRec(n-i))%mod )%mod;

}

return ans;

}

long long solveMem(int n, vector<long long>& dp)

{

if(n<=1)

return 1;

if(dp[n] != -1)

return dp[n];

long long ans = 0;

// think i as root node

for(int i=1; i<=n; i++) {

ans = ( ans + (solveMem(i-1, dp) * solveMem(n-i, dp))%mod )%mod;

}

return dp[n] = ans;

}

long long solveTab(int n)

{

vector<long long> dp(n+1, 0);

dp[0] = dp[1] = 1;

// i -> number of nodes

for(int i=2; i<=n; i++) {

// j-> root nodes

for(int j=1; j<=i; j++) {

dp[i] = ( dp[i] + (dp[j-1] * dp[i-j])%mod )%mod;

}

return dp[n];

}

long long totalTrees(int num)

{

// return solveRec(num);

// vector<long long> dp(num+1, -1);

// return solveMem(num, dp);

return solveTab(num);

}

programming

100daysofcode

beginners

datastructures

169 views

0 replies

2 upvotes

Surbhi Shekhar

Interview problems

c++

long long totalTrees(int n){

// Write your code here.

long long int mod=1e9+7;

vector<long long int> dp(n+1);

dp[0]=1;

for(int i=1;i<=n;i++)

{

long long int sum=0;

for(int j=0;j<i;j++)

{

sum+=(dp[j]*dp[i-j-1])%mod;

}

dp[i]=sum%mod;

}

return dp[n];

}

151 views

0 replies

1 upvote

monish

Interview problems

python solution

def totalTrees(n):
    mod = 10**9 + 7
    dp = [0] * (n + 1)
    dp[0] = 1

    for i in range(1, n + 1):
        total_sum = 0
        for j in range(i):
            total_sum += (dp[j] * dp[i - j - 1]) % mod
        dp[i] = total_sum % mod

    return dp[n]

python

90 views

0 replies

0 upvotes

Prince Pandey

Interview problems

c++ solution

long long totalTrees(int n){

// Write your code here.

long long int mod=1e9+7;

vector<long long int> dp(n+1);

dp[0]=1;

for(int i=1;i<=n;i++)

{

long long int sum=0;

for(int j=0;j<i;j++)

{

sum+=(dp[j]*dp[i-j-1])%mod;

}

dp[i]=sum%mod;

}

return dp[n];

}

148 views

0 replies

0 upvotes

Randeep Sarma

Interview problems

Don't know if that is optimised or not





long long funct(int n,vector<long long>&dp){
if(n==0 || n==1)return 1;
if(n==2)return 2;
    if(dp[n]!=-1)return dp[n];
int mod=1e9+7;    
long long total=0;
for(int i=0;i<n/2;i++){
    total=(total+(2*(funct(i,dp)*funct(n-1-i,dp))%mod)%mod)%mod;
}    
if(n%2==1){
    total=(total+(funct(n/2,dp)*funct(n/2,dp))%mod)%mod;
}    
    return dp[n]=total;
}

long long totalTrees(int num){
    // Write your code here.
    vector<long long>dp(num+1,-1);
    return funct(num,dp);
}