Last Updated: 7 Dec, 2020
Check Bipartite Graph
Moderate
Asked in companies



Given a graph, check whether the graph is bipartite or not. Your function should return true if the given graph's vertices can be divided into two independent sets, ‘U’ and ‘V’ such that every edge (‘u’, ‘v’) either connects a vertex from ‘U’ to ‘V’ or a vertex from ‘V’ to ‘U’.
You are given a 2D array ‘edges’ which contains 0 and 1, where ‘edges[i][j]’ = 1 denotes a bi-directional edge from ‘i’ to ‘j’.
Note:
If edges[i][j] = 1, that implies there is a bi-directional edge between ‘i’ and ‘j’, that means there exists both edges from ‘i’ to ‘j’ and to ‘j’ to ‘i’.
For example
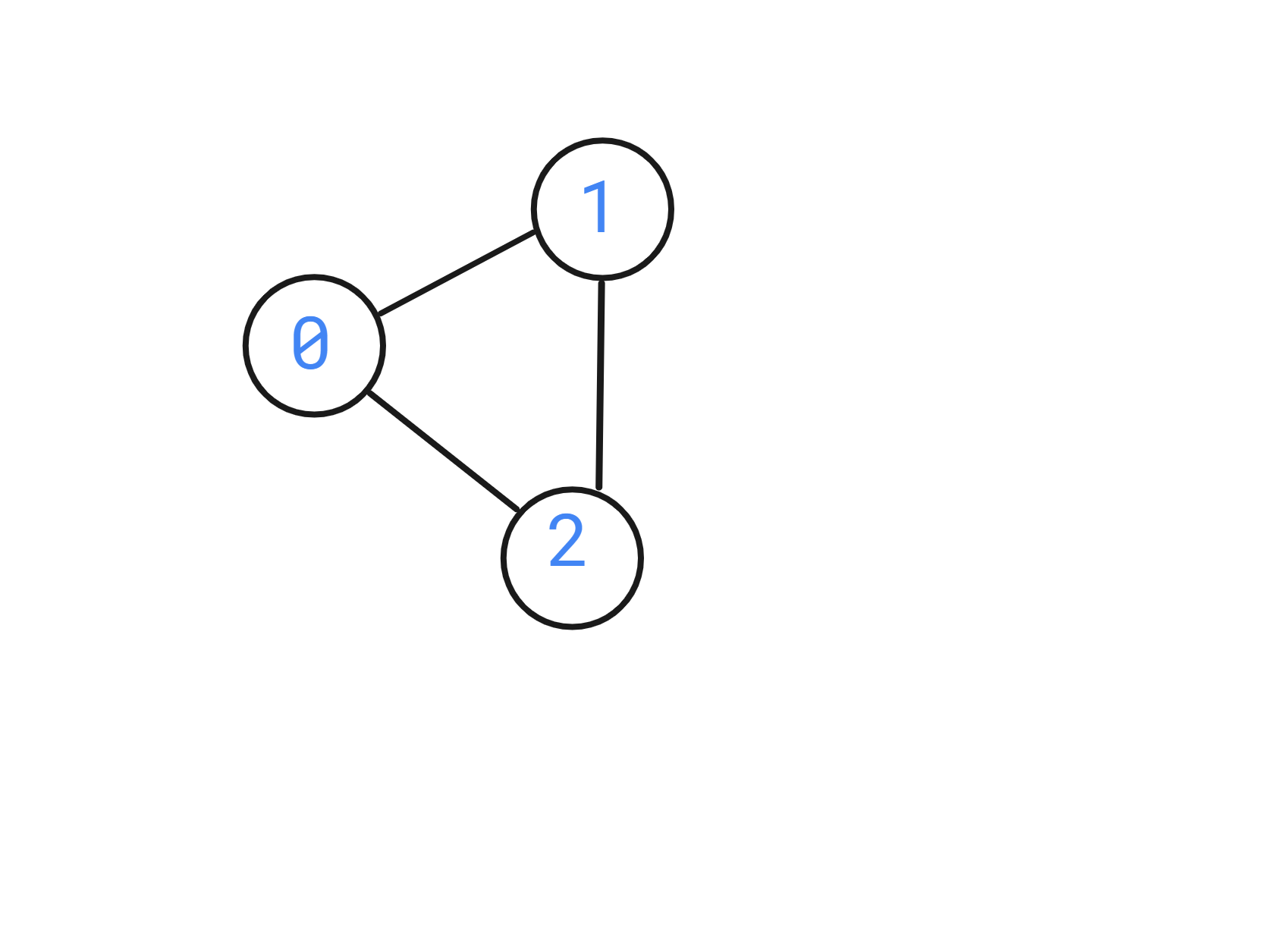
Given:
‘N’ = 3
‘edges’ = [[0, 1, 1], [0, 0, 1], [0,0,0]].
Input format:
The first line of input contains an integer ‘T’ denoting the number of test cases.
The first line of each test case contains two space-separated integers, ‘N,’ where ‘N’ is the number of rows in ‘edges’ and the number of columns in ‘edges’.
The next ‘N’ line of each test case contains ‘N’ space-separated integers which tell if there is an edge between ‘i’ and ‘j’.
Output Format :
For each test case, You are supposed to return a bool value determining whether the graph is bipartite or not.
Note:
You are not required to print the expected output; it has already been taken care of. Just implement the function.
Constraints:
1 <= ‘T’ <= 10
2 <= ‘N’ <= 300
0 <= ‘edges[i][j]’ <= 1.
Time Limit: 1sec.
Approaches
The idea is that a bipartite can be colored in such a way that only 2 colors in total would be used, where the neighbor nodes have different colors. Therefore we can do a breadth-first search and assign colors to each vertex and if at any point neighboring nodes have the same color we return false.
The steps are as follows:
- Parse the given ‘edges’ into an adjacency matrix ‘graph’, by pushing ‘i’ is graph[j] and ‘j’ in graph[i] if edges[i][j] is 1.
- Maintain a vector ‘color’ which denotes the color of the ‘i’ the node, initially, all colors are un-assigned, hence -1.
- Maintain a color ‘c’ initially 0 to assign to nodes and flip after each level of the graph.
- Now maintain a queue ‘que’ for doing a breadth-first traversal and push ‘i’, the root node in it.
- While ‘que’ is not empty:
- Maintain a variable ‘node’ which denotes the node in the front of the ‘que’.
- Traverse all the neighbors ‘nbr’ of the current node.
- If the ‘color[nbr]’ is equal to ‘color[node]’, return false, since this is not possible, as discussed above.
- Else if the ‘color[nbr]’ is -1, which means it is unassigned, assign it ‘c’.
- Flip the color after traversing all the ‘nbr’ of ‘node’.
- If we exit the loop, return true, since all nodes have been assigned colors and no 2 adjacent nodes have the same color.

