Last Updated: 13 Nov, 2020
Copy List with Random Pointer
Easy
Asked in companies



Given a linked list having two pointers in each node. The first one points to the next node of the list, however, the other pointer is random and can point to any node of the list or null. The task is to create a deep copy of the given linked list and return its head. We will validate whether the linked list is a copy of the original linked list or not.
A deep copy of a Linked List means we do not copy the references of the nodes of the original Linked List rather for each node in the original Linked List, a new node is created.
For example,
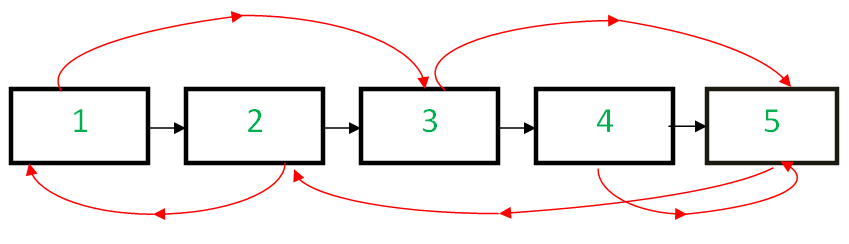
Random pointers are shown in red and next pointers in black.
Input Format:
The first line of input contains an integer ‘T’ representing the number of test cases. Then the test cases follow.
The only line of each test case contains the elements of the linked-list with random pointers. The line consists of nodes (value of node followed by its random pointer) separated by a single space. In case a node (next or random pointer) is null, we take -1 in its place.
Each node is represented as a pair of a value and its random index where,
Value: an integer representing the value of the node
Random index: the index of the node where the random pointer points to, or -1 if it does not point to any node.
For example, the input for the linked list depicted in the below image would be:

1 2 2 0 3 4 4 4 5 1 -1
Explanation:
The head node of the linked-list is 1, and its random pointer points to a node present at index 2, i.e. node 3.
The second node of the linked list is 2, and its random pointer points to a node present at index 0, i.e. node 1.
In this way, input for each node is taken until a pair having its first part as -1 is encountered since it denotes a node having null value, i.e. end of the linked list.
Output Format:
For each test case, the only output line contains “true” if the linked list is successfully cloned.
The output for each test case is in a separate line.
Note:
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10 ^ 2
0 <= N <= 10 ^ 3
0 <= DATA <= 10 ^ 6 and data != -1
-1 <= RANDOMINDEX < N
Where ‘T’ is the number of test cases, ‘N’ is the total number of nodes in the linked list, 'DATA' is the value of the linked list node and 'RANDOMINDEX' is the index of the node where the random pointer points to.
Time limit: 1 sec.
Follow up:
Can you do it without using extra space?
Approaches
The basic idea behind the recursive solution is to consider the linked list like a binary tree. Every node of the Linked List has 2 pointers. So we consider these nodes as belonging to a binary tree. The head of the list becomes the root of the tree. So what we basically have to do now is to traverse the binary tree and clone it. The main issue that we need to tackle here is that of loops. So we can have, 1 1 2 0 -1, we need to handle this in the code.
We start from the root node, and we keep traversing the tree (list), and we keep generating new nodes whenever we find a node for which the clone has not been generated. For example, we were at node A, and we used the next pointer to go to node B, and we created B’, which is a new node B with the same data. Also, say there was a random pointer from A to B. In this case, we don’t have to create yet another copy of node B because B’ already exists. We need to take care of this as well.
Steps are as follows:
- Base case: If the current node is not present in the linked list, return null.
- Check if we have already processed the current node (using HashMap), then simply return the cloned version of it.
- Else, create a new node with the data same as the old node, i.e. copy the node.
- Save this value in the HashMap. This is needed to avoid the loops which might be there while traversing the list.
- Recursively copy the remaining linked list starting once from the next pointer and then from the random pointer.
- Finally, update the next and random pointers for the new node created and return it.
The iterative solution to this problem does not model it as a tree and instead simply treats it as a LinkedList. The idea is to use Hashing. Below is the algorithm:
- We can solve this problem in two passes.
- In the first pass over the original list, we can create an exact clone of the list with consistent next pointers. Note that the random pointers are not yet cloned.
- Additionally, we have a HashMap that maintains the old node to new node mapping. We will need it later on.
- In the second pass, we clone the random pointer. The way we do it like this. The random pointer for ‘A’ ('A' is the cloned version of node A) is the HashMap value of the node pointed to by the random pointer of A.
To optimize the space complexity, we should think of another approach. To reduce the additional space used we will proceed as follows:
1. Create the COPY of NODE1 and insert it between NODE1 & NODE2 in the ORIGINAL linked list. Similarly, create the COPY of node 2 and insert it between NODE2 & NODE3 and so on. Insert the COPY of the Nth node after the Nth node.
2. Now COPY the random link in this fashion
ORIGINAL -> next -> random = ORIGINAL -> random -> next
This works because ORIGINAL -> next is nothing but a COPY of ORIGINAL and ORIGINAL -> random -> next is nothing but a COPY of random.
3. Now restore the ORIGINAL and COPY linked lists in this fashion in a single loop.
- ORIGINAL -> next = ORIGINAL -> next -> next;
- COPY -> next = COPY -> next -> next;
4. Make sure that ORIGINAL -> next is NULL and return the cloned linked list.

