Last Updated: 26 Dec, 2020
Connect Nodes at Same Level
Moderate
Asked in companies



A binary tree is a tree where each node has at most two children i.e left child and right child.
You are given a binary tree, where the structure of the node is as follow -:
class BinaryTreeNode {
int data; // Value of the node.
BinaryTreeNode *left; // Pointer to left child node.
BinaryTreeNode *right; // Pointer to right child node.
BinaryTreeNode *next; // Pointer to next right node at same level.
}
Your task is to connect all the adjacent nodes at the same level in the given binary tree. You can do this by populating each 'next' pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL. Initially, all the next pointers are set to NULL.
For Example:
Consider the figure shown below. The left part represents the initial binary tree and right part represents the binary tree after connecting adjacent nodes at the same level.
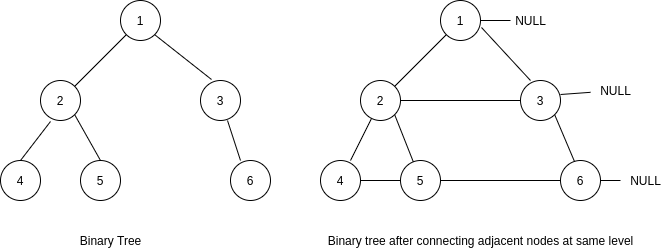
In the tree shown in the picture above -:
The ‘next’ pointer of the node having value 2 is connected to the node having value 3.
The ‘next’ pointer of the node having value 4 is connected to the node having value 5.
The ‘next’ pointer of the node having value 5 is connected to the node having value 6.
The ‘next’ pointer of nodes having value 1, 3, 6 will have a value NULL as there are no next right nodes in their cases.
Note:
1. The structure of the ‘Node’ of a binary tree is already defined. You should not change it.
2. The root of the binary tree is known to you.
3. There is at least one node in the given binary tree.
4. You may only use constant extra space.
Input format:
The first line of input contains an integer ‘T’ denoting the number of test cases.
Then the description of ‘T’ test cases follows.
The first line of each test case contains elements in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.
For example, the input for the tree depicted in the below image would be :
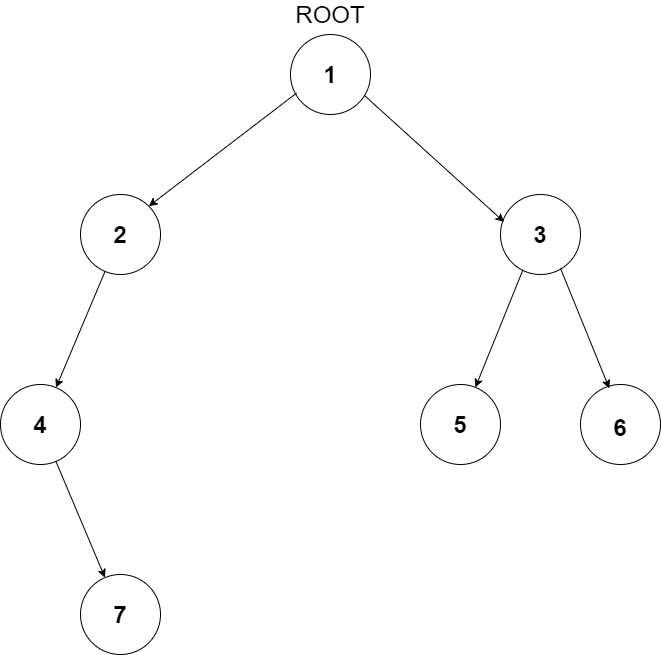
1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 2
Right child of 1 = 3
Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6
Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)
Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)
The first not-null node (of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
The input ends when all nodes at the last level are null (-1).
Note :
The above format was just to provide clarity on how the input is formed for a given tree.
The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1
Output format :
For each test case, print the level order as connected by the next pointers, with '#' signifying the end of each level.
Note:
You do not need to print anything, it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 100
1 <= N <= 3000
-10^9 <= DATA <= 10^9
Where ‘T’ is the total number of test cases, ‘N’ is the number of nodes in the given binary tree and 'DATA' is the value in each node.
Time Limit: 1 sec
Approaches
Approach: In the Level order traversal or breadth first traversal of the tree, we traverse all the nodes at each level before going to the next level. We can extend level order traversal to solve this problem as follows.
Algorithm is as foolows:
- Create a queue and enqueue the address of the given root node in it.
- Initialize an integer variable ‘NODECOUNT’ = 1, it will represent the number of nodes in the current level of the binary tree.
- Run a while loop till queue not become empty and in each iteration perform following steps -:
- Create a pointer ‘PREVIOUS’ and initialize it by NULL.
- Run a loop while loop till ‘nodeCount’ is greater than 0. And in each iteration of this while loop do following:
- If ‘PREVIOUS’ is not NULL. then assign the address of the front node of the queue to the ‘NEXT’ pointer of the node represented by the ‘PREVIOUS’ pointer.
- Assign address of the front node of the queue to the ‘PREVIOUS’ pointer.
- Dequeue the node at the front of the queue, and enqueue its left and right child (if exist).
- Decrement ‘NODECOUNT’ by 1.
- The queue will now have all the nodes of the next level. Assign size of the queue to the variable ‘NODECOUNT’.
Approach: Suppose we have already populated the ‘NEXT’ pointers till level ‘L’. Now we can iterate over level ‘L’ using ‘NEXT’ pointers and populate ‘next’ pointers in level ‘L + 1’.
It can be implemented as follow:
- Create a pointer ‘STARTNODE’ and initialize it by the address of the given root node. The pointer ‘STARTNODE’ will keep the address of the first node of the current level.
- Run a while loop till ‘STARTNODE’ is not equal to NULL, and in each iteration do following:
- Create a pointer ‘PTR’ and assign the value of ‘STARTNODE’ to it, we will use this pointer ‘PTR’ to iterate over nodes of the current level.
- Assign the address of the first node of next level to ‘STARTNODE’, if there is no next level then assign NULL to it.
- Iterate over the current level using the pointer ‘PTR’, the next level is formed by the left or right child of the nodes of the current level, so while iterating you can keep track of nodes encountered on the next level from left to right and connect them accordingly.
- All the next pointers will be populated after this while loop.

