Last Updated: 29 Aug, 2021
Depth of BST
Moderate
Asked in company

You are given an array ‘ARR’ having ‘N’ elements ranging from 1 to ‘N’.Each number appears in the array only once. Your task is to find the maximum depth of the Binary Search Tree formed if these values are inserted into the tree in the given order.
For Example
If 'ARR' is [2,1,4,3] ,the formed tree will be:
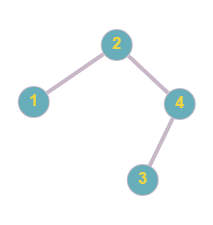
The maximum depth of the tree is 3. Hence the answer is 3.
Input Format:
The first line of the input contains an integer, 'T,’ denoting the number of test cases.
The first line of each test case contains a single integer, 'N,’ denoting the number of elements in ‘ARR’.
The next line of each test case has ‘N’ integers corresponding to the elements of 'ARR’.
Output Format:
For each test case, return a single integer corresponding to the maximum depth of the BST.
Note:
You do not need to print anything. It has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 10
1 <= N <= 10^5
1 <= 'ARR'[i] <= N
Time limit: 1 sec
Approaches
In this approach, we will prepare an array 'DEPTH' to store the depth of all values in the BST.
We will store the values in sorted order in an ordered Set as insertion, deletion, and searching takes O(logN) time. We will iterate through all values and search for the value 'VAL' in the set whose value is just greater than the current value and set the depth of the current value as the depth of 'VAL' + 1, and we will also store the maximum depth in a variable.
Algorithm:
- Declare an integer 'ANS' to store the maximum depth and initialize it with 0.
- Declare an array 'DEPTH' of size 'N'+1 to store the depth of all values.
- Declare an ordered set 'VALUES' to store the values in sorted order.
- Set 'DEPTH' of 'ARR'[0] as 1.(Root Node of BST)
- Insert 'ARR'[0] into 'VALUES'.
- For each index IDX in range 1 to 'N'-1, do the following:
- Set 'VAL' as the value in an ordered set whose value is just greater than V[i].
- If no such value exists , set 'VAL' as the maximum value present in the ordered set.
- Set 'DEPTH'[ 'ARR'[IDX] ] as depth of 'VAL' +1.
- Set 'ANS' as the maximum of 'ANS' and 'DEPTH'[ 'ARR'[IDX] ].
- Insert 'ARR'[IDX] into 'VALUES'.
- Return 'ANS'.

