Last Updated: 7 Feb, 2021
Longest Repeating Subsequence
Moderate
Asked in companies



You are given a string ‘st’, Your task is to find the length of the longest repeating subsequence such that two subsequences don’t have the same character at the same position.
For Example :
The given string st = AABCBDC.
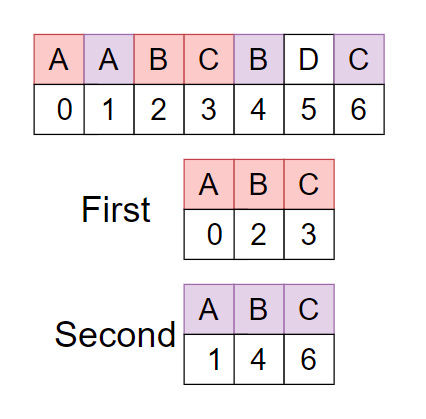
As you can see there are two repeating longest subsequences “ABC” with the same character but different position. Therefore the required answer is ‘3’ as the length of “ABC” is 3.
Input Format :
The first line of input contains an integer ‘T’ denoting the number of test cases.
The first line of each test case contains a single integer ‘N’, where ‘N’ denotes the length of string ‘st’.
The second line of each test case contains a string ‘st’.
Output Format :
For every test case, print the length of the longest repeating subsequence.
Output for each test case will be printed in a separate line.
Note :
You do not need to print anything; it has already been taken care of. Just implement the given function.
All the characters of the given string ‘st’ are uppercase letters.
Constraints :
1 <= T <= 50
1 <= N <= 100
Time Limit: 1 sec
Approaches
The basic idea is the same as the longest common subsequence( LCS), only need to exclude the case when (i==j) because we can’t consider both same characters in both the subsequence.
Follow this step-
LRS[i][j] = LRS[i-1][j-1] +1 where ( st[i-1] == st[j-1] and i!=j)
LRS[i][j] = max(LRS[i-1][j], LRS[i][j-1]) where ( st[i-1] != st[j-1)
Consider base case if(i==0 and j==0) then LRS[0][0]=0
Algorithm
- LRSHelper( st , i, j), to return longest repeating subsequence
- if(i==0 or j==0 ), base case
- Return 0
- if( st[i-1] == st[j-1] and (i!=j) )
- Return LRS[i][j] = LRS[i-1][j-1] +1
- Else
- Return max(LRS[i-1][j], LRS[i][j-1])
There were many overlapping sub-problems in the recursive approach. This can be solved using the memoization technique.
The idea is that compute LRS[i][j] and store the answer of LRS[i][j] in an array and use it for all the other calls of LRS[i][j]
Algorithm
- Use a 2-D array ‘dp’, to store the answer of every (i and j)
- LRSHelper( st , i, j), to return longest repeating subsequence
- If ( answer of LRS[i][j] is present in array)
- Then return answer of LRS[i][j]
- Else compute the answer for LRS[i][j] same as previous approach
- if(i==0 or j==0 ), base case
- dp[ LRS[i][j] ] =0
- Return 0
- if( st[i-1] == st[j-1] and (i!=j) )
- dp[ LRS[i][j] ] = LRS[i-1][j-1] +1
- Return dp[ LRS[i][j] ]
- Else
- dp[ LRS[i][j] ] = max(LRS[i-1][j], LRS[i][j-1])
- Return dp[ LRS[i][j] ]
Create a dp table and with the same idea as discussed in approach1.
Follow this step-
dp[i][j] = dp[i-1][j-1] +1 where ( st[i-1] == st[j-1] and i!=j)
dp[i][j] = max(dp[i-1][j], dp[i][j-1]) where ( st[i-1] != st[j-1)
Algorithm
- Create a 2-d ‘dp’ table of size ‘(n+1)*(n+1)’ with initial value ‘0’.
- Iterate a loop ‘i’ from ‘1’ to ‘n’
- Iterate another nested loop ‘j’ from ‘1’ to ‘n’
- if (st[i - 1] == st[j - 1]) and i!=j
- dp[i][j] = dp[i - 1][j - 1]+1
- Else
- dp[i][j] = max( dp[i - 1][j], dp[i][j - 1])
- if (st[i - 1] == st[j - 1]) and i!=j
- Iterate another nested loop ‘j’ from ‘1’ to ‘n’
- Return dp[n][n]

