Last Updated: 25 Apr, 2021
Minimum Time To Visit All Points
Moderate
Asked in companies



Ninja lives in a 2D plane where each location is represented with integer coordinates ‘[X, Y]’. You are given an array ‘POINTS’ containing ‘N’ such points. Ninja lives at the location ‘POINTS[0]’ and wants to visit all the remaining ‘N-1’ points in the order given by the ‘POINTS’ array. Your task is to help ninja find the minimum time (in seconds) required to visit all the points in the given order (starting from ‘POINTS[0]’).
The ninja can travel according to the following rules :
- In one second, the ninja can either:
- Move vertically by one unit, i.e., along the y-direction.
- Move horizontally by one unit, i.e., along the x-direction.
- Move diagonally by ‘sqrt(2)’ units, i.e., move one unit horizontally then one unit vertically.
- The ninja must visit the points in the exact order as they are given the ‘POINTS’ array.
- The ninja is allowed to pass through points that may be given later in the order, but these points will not be counted as visited.
- Move vertically by one unit, i.e., along the y-direction.
- Move horizontally by one unit, i.e., along the x-direction.
- Move diagonally by ‘sqrt(2)’ units, i.e., move one unit horizontally then one unit vertically.
For Example :
‘POINTS = [ [3, 1], [-1, 3], [2, 0] ]’, ‘N = 3’
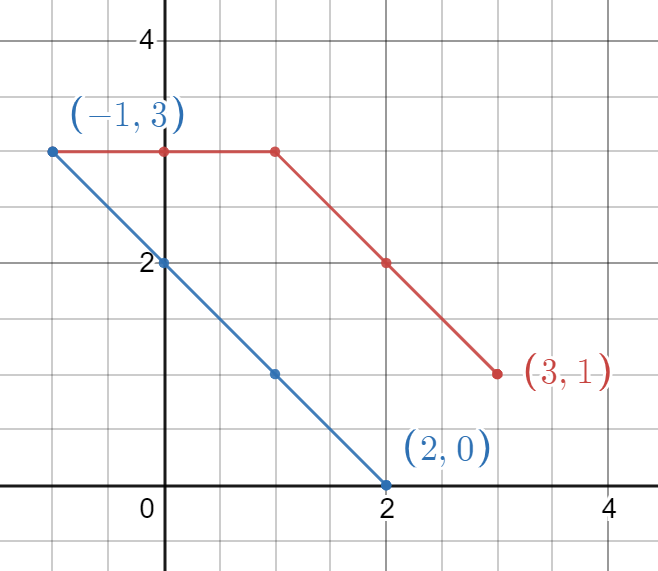
The path with minimum time is: ‘[3,1] -> [2,2] -> [1,3] - > [0,3] -> [-1,3] -> [0,2] -> [1,1] -> [2,0]’.
Time taken from [3,1] to [-1,3] = 4 seconds.
Time taken from [-1,3] to [2,0] = 3 seconds.
Total time = 7 seconds. Thus, you should return ‘7’ as the answer.
Input Format :
The first line of input contains an integer ‘T’ which denotes the number of test cases. Then, the ‘T’ test cases follow.
The first line of each test case contains an integer ‘N’ denoting the number of points. Then, ‘N’ lines follow.
Each line contains two integers, ‘X’ and ‘Y’, representing an element of the array ‘POINTS’.
Output Format :
For every test case, the minimum time to visit all the points in the given order.
Note :
You do not need to print anything; it has already been taken care of. Just implement the function.
Constraints :
1 <= T <= 100
1 <= N <= 1000
Each element of ‘POINTS’ contains exactly two integers ranging from [-10^5, 10^5].
Time limit: 1 second
Approaches
As per the problem, moving ‘sqrt(2)’ units diagonally is equivalent to (moving ‘1’ unit horizontally + moving ‘1’ unit vertically). The same distance covered diagonally in ‘1’ second requires ‘2’ seconds otherwise (‘1’ second for horizontal and ‘1’ second for vertical). Therefore, we should move diagonally as much as possible for optimal movement, and we should cover the remaining distance either horizontally or vertically.
Consider the following example where we move from point ‘[X1, Y1]’ to ‘[X2, Y2]’:
When we move ‘sqrt(2)’ units diagonally, we also move the ‘1’ unit along the x-direction or the y-direction.
Thus, the time required to move diagonally from ‘[X1, Y1] to [X3, Y2] = X3 - X1’.
Time required to move horizontally from ‘[X3, Y2] to [X2, Y2] = X2 - X3’.
Therefore, the time required to move from ‘[X1, Y1] to [X2, Y2] = (X3-X1)+(X2-X3) = X2-X1’.
If negative coordinates are present, we have the required time as ‘abs(X2 - X1)’ (absolute value).
Notice that here ‘abs(X2 - X1) > abs(Y2 - Y1)’ meaning we have to move diagonally and then horizontally. So, if ‘abs(Y2 - Y1) > abs(X2 - X1)’, then we have to move diagonally and then vertically, and the time required will be ‘abs(Y2 - Y1)’.
Thus, the minimum time required to travel from point,
‘[X1, Y1] to [X2, Y2] = max(abs(X2 - X1), abs(Y2 - Y1))’.
Algorithm
- Set ‘RES = 0’. Use it to store the time required for visiting all the points.
- Run a loop where ‘i’ ranges from ‘1’ to ‘N-1’:
- ‘X1 = POINTS[i - 1][0]’ and ‘Y1 = POINTS[i - 1][1]’. Coordinates of point ‘i-1’.
- ‘X2 = POINTS[i][0]’ and ‘Y2 = POINTS[i][1]’. Coordinates of point ‘i’.
- ‘RES += max(abs(X1 - X2), abs(Y1 - Y2))’. Minimum time required to travel from point ‘i - 1’ to point ‘i’.
- Return ‘RES’ as the answer.

