Last Updated: 11 Jan, 2021
Pascal's Triangle
Easy
Asked in companies



You are given an integer N. Your task is to return a 2-D ArrayList containing the pascal’s triangle till the row N.
A Pascal's triangle is a triangular array constructed by summing adjacent elements in preceding rows. Pascal's triangle contains the values of the binomial coefficient. For example in the figure below.
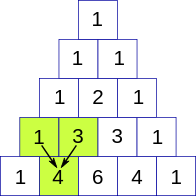
For example, given integer N= 4 then you have to print.
1
1 1
1 2 1
1 3 3 1
Here for the third row, you will see that the second element is the summation of the above two-row elements i.e. 2=1+1, and similarly for row three 3 = 1+2 and 3 = 1+2.
Input format :
The first line of input contains an integer ‘T’ denoting the number of test cases.
The first line of each test case contains a single integer N denoting the row till which you have to print the pascal’s triangle.
Output format :
For each test case, return the 2-D array/list containing the pascal’s triangle till the row N.
Note:
You do not need to print anything; it has already been taken care of. Just implement the given function.
Constraints:
1 <= T <= 40
1 <= N <= 50
Time Limit: 1 sec
Approaches
The idea is to use recursion to get the value of the coefficients we will create a helper function CALPASCAL which will take row and entry as its input parameters and we call this function in the main function of PRINTPASCAL.
- Inside the function CALPASCAL if the row is 0 or the entry is equal to row then we will just return 1.
- Else we will return the sum of adjacent previous row value that is CALPASCAL(I-1,J-1) + CALPASCAL(I-1,J).
- Now for the main function to store the pascal’s triangle PRINTPASCAL inside this declare a 2-D arrayList TRIANGLE and run loop from row I=0 to I<N.
- Inside this loop run a loop from entry J=0 till entry J=R.
- Inside this loop calculate the answer for each entry by calling the CALPASCAL function and add it to the arraylist.
- Finally return the arraylist.
The idea is to use the definition of pascal’s triangle that its coefficients and are summation of adjacent elements in preceding rows. so in this way we can store the elements in a matrix and for further generation of values in it we can check the preceding elements and update the value.
- Declare an ArrayList of arraylist TRIANGLE to store the elements values.
- Run a loop from row R =0 till N-1.
- Now inside this loop run one more loop from value J=0 till J<=R.
- If the number is first or last one then just store 1 in the matrix i.e. TRIANGLE[R][J]=1.
- Else store the sum of adjacent elements in preceding rows i.e. TRIANGLE[R][J]=TRIANGLE[R-1][J-1] + TRIANGLE[R-1][J].
- Print this value i.e. the value in the current iteration TRIANGLE[R][J].
- Finally return the arrayList
The idea is to use the property of pascal’s triangle that its coefficients and are nothing but the binomial coefficients so we will calculate binomial coefficients of each line and at each index and print them, the coefficient value at every index is nCr where n is equal to the current row number and r is the rth entry in the row n and its value is FACT(n)/(FACT(n-r)*FACT(r)) where FACT(X) is the factorial of the number X but in this approach, we will use maths to derive the relation between Eth entry ‘RCE’ and (E-1)th entry RC(E-1)
- So RCE and RC(E-1)
- RCE = FACT(R)/(FACT(R-E)*FACT(E)) and RC(E-1)= FACT(R)/(FACT(R-E+1)*FACT(E-1)) after simplifying and comparing we get
- RCE = RC(E-1) * (R-E+1)/E.
- Declare an ArrayList of ArrayList TRIANGLE to store the values of the elements.
- Now run a loop from row R=1 to R=N.
- Inside this initialize RCE=1 that represents rCe.
- Inside this loop run a loop from entry E=1 till entry E=R. Store RCE in the ArrayList and update RCE to RCE*(ROW - E)/E.
- Finally, return ArrayList.

