Last Updated: 20 Jan, 2022
Postorder Traversal
Easy
Asked in companies


You have been given a Binary Tree of 'N' nodes, where the nodes have integer values. Your task is to find the Post-Order traversal of the given binary tree.
For example :
For the given binary tree:
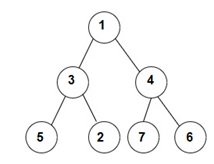
The Postorder traversal will be [5, 2, 3, 7, 6, 4, 1].
Input Format :
The first line contains an integer 'T' which denotes the number of test cases.
The first and only line of each test case contains elements of the tree in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.
Example :
The input for the tree is depicted in the below image:
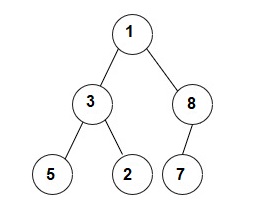
1 3 8 5 2 7 -1 -1 -1 -1 -1 -1 -1
Explanation :
Level 1 :
The root node of the tree is 1
Level 2 :
Left child of 1 = 3
Right child of 1 = 8
Level 3 :
Left child of 3 = 5
Right child of 3 = 2
Left child of 8 =7
Right child of 8 = null (-1)
Level 4 :
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 2 = null (-1)
Right child of 2 = null (-1)
Left child of 7 = null (-1)
Right child of 7 = null (-1)
1
3 8
5 2 7 -1
-1 -1 -1 -1 -1 -1
Note :
1. The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.
2. The input ends when all nodes at the last level are null(-1).
3. The above format was just to provide clarity on how the input is formed for a given tree. The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:
1 3 8 5 2 7 -1 -1 -1 -1 -1 -1 -1
Output Format :
For each test case, return a vector containing the Post-Order traversal of a given binary tree.
The first and only line of output of each test case prints 'N' single space-separated integers denoting the node's values in Post-Order traversal.
Note :
You don't need to print anything, it has already been taken care of. Just implement the given function.
Constraints :
1 <= T <= 10
0 <= N <= 3000
0 <= data <= 10^9
Where 'data' denotes the node value of the binary tree nodes.
Time limit: 1 sec
Approaches
As we can see, before processing any node, the left subtree is processed first, followed by the right subtree, and the node is processed at last. These operations can be defined recursively for each node. The recursive implementation is referred to as a Depth-first search (DFS), as the search tree is deepened as much as possible on each child before going to the next sibling.
The steps are as follows :
- We create a recursive function postOrderHelper() which takes the root of the tree as an argument.
- postOrderHelper() :
- Visit the left subtree of ‘node’ i.e., call postOrderHelper(‘node’ -> left).
- Visit the right subtree of ‘node’ i.e., call postOrderHelper(‘node’ -> right).
- Visit ‘node’ and if ‘node’ != NULL then add data of node to answer.
To convert the above recursive procedure into an iterative one, we need an explicit stack.
The steps are as follows :
- Create an empty stack and answer list.
- Initialize the current node as root, and push the current node to stack.
- Run a loop until the stack is not empty and do :
- Pop-top node from the stack and set the popped node as the current node.
- Add data of the current node to the answer list.
- Push the left child of the current node to stack.
- Push the right child of the current node to stack.
- At last reverse all elements of the answer list.
The idea here is to use Morris traversal for the Postorder traversal of the tree. The idea of Morris's traversal is based on the Threaded Binary Tree. In this traversal, we will create links to the predecessor back to the current node so that we can trace it back to the top of a binary tree. Here we don’t need to find a predecessor for every node, we will be finding a predecessor of nodes with only a valid left child.
So Finding a predecessor will take O( N ) as time as we will be visiting every edge at most two times and there are only ‘N’ - 1 edges in a binary tree. Here ‘N’ is the total number of nodes in a binary tree.
For more details, please check the Threaded binary tree and Explanation of Morris Method
The steps are as follows :
- The basic idea is that postorder traversal can be considered as the reverse process of preorder traversal.
- Create a new node, say ‘CURRENT’, and initialize it as ‘ROOT’.
- Run a loop until ‘CURRENT’ != NULL and do:
- If the right child of ‘CURRENT’ is NULL then add ‘CURRENT’ node data to answer and do CURRENT = CURRENT -> left.
- Else make a left child of inorder predecessor point to the ‘CURRENT’ node, then the following two cases will occur:
- If the left child of inorder predecessor points to the ‘CURRENT’ node then set left child = NULL and visit the left child of the current node i.e., CURRENT = CURRENT -> left.
- If the left child is NULL then set it to the current node. Add data of the current node to answer and move to the right child of the current node i.e., CURRENT = CURRENT -> right.
- Hence we just need to change left child to right child and always insert data of node at beginning of our answer. We can achieve this by inserting data of node at end of answer array and then reverse elements of our answer array.
Similar problems

