Last Updated: 5 Apr, 2021

Travelling Salesman Problem

Hard

Asked in companies

Solve now

Problem statement

Given a list of cities numbered from 0 to N-1 and a matrix 'DISTANCE' consisting of 'N' rows and 'N' columns denoting the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the starting city?

Input Format :

The first line contains a single integer ‘T’ denoting the number of test cases. The test cases are as follows.

The first line of each test case contains an integer ‘N’, where ‘N’ denoting the number of the cities.

The next ‘N’ lines of each test case contain ‘N’ space-separated integers “DISTANCE[i][j]”, where DISTANCE[i][j] denotes the distance to jth city from the ith city.

Output Format :

For each test case, return the minimum distance of the shortest possible route which visits each city exactly once and returns to the starting city.

Note :

You don’t need to print anything; It has already been taken care of. Just implement the given function.

Constraints :

1 <= T <= 5
2 <= N <= 16
0 <= DISTANCE[i][j] <= 10^9

Time Limit: 1 sec

Solve now

Approaches

01 Approach

The idea here is to visit all possible permutations of visiting the vertex.

Example-

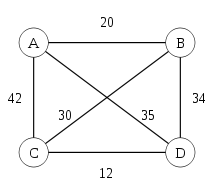
Consider the above graph one possible permutation is A -> B -> C -> D -> A. Similarly we try all permutations and calculate the cost of each of the routes and update the 'ANS' to a minimum such route.

If we notice B -> C -> D -> A -> B is a cyclic permutation of A -> B -> C -> D -> A. All the cyclic permutations will lead to the same 'ANS'wer. So, we can fix a particular vertex, say A and try for remaining (N - 1)! permutations.

We also need to keep in mind whether a particular vertex is visited or not. If it's visited then we don’t need to revisit them.

There are many options to solve this problem, we can have an array of size ‘N’ and each element is either 0 or 1, 0 denoting the 'CITY' is visited and 1 denoting the 'CITY' is not visited. Here since the number of vertices is very less we can represent this array visited as a 'MASK' with ‘N’ bits, each bit corresponds to whether a particular 'CITY' is visited or not. If the i-th bit is set in the 'MASK' then the i-th 'CITY' is already visited, otherwise, the i-th 'CITY' is not visited. If the 'MASK' is equal to (1 << N) - 1 then this 'MASK' corresponds to all the cities being visited.

So, the recurrence to the above problem is:

GET_MIN_DISTANCE('MASK', 'CURRENT_CITY') = min ∀ 'CITY' (DISTANCE['CURRENT_CITY']['CITY'] + GET_MIN_DISTANCE('MASK' | (1 << 'CITY'), 'CITY').

Where, GET_MIN_DISTANCE('MASK','CURRENT_CITY') calculates the minimum distance to reach 'CURRENT_CITY' with set bits of 'MASK' denoting the cities visited till now.

Where 'MASK' | (1 << 'CITY') sets the 'CITY'-th bit in 'MASK' i.e mark the 'CITY' as visited and DISTANCE['CURRENT_CITY']['CITY'] is the distance of 'CURRENT_CITY' to 'CITY'.

The algorithm is:

Declare a function GET_MIN_DISTANCE with parameters 'MASK' and 'CURRENT_CITY', where 'MASK' stores the information of the cities that are currently visited and 'CURRENT_CITY' denoted 'CITY' from where we want to calculate the shortest route.
- If the 'MASK' is equal to (1 << N) - 1.
  - Return DISTANCE['CURRENT_CITY'][0], since we have fixed 'CITY' 0 and now we just need to return the cost of the path 'CURRENT_CITY' -> 0.
- Declare an integer variable 'ANS' and set it to INFINITY.
- Iterate from 'CITY' = 0 to N - 1,
  - If the 'MASK' & (1 << 'CITY') == 0, i.e the 'CITY'-th bit is unset in 'MASK' and this 'CITY' is unvisited.
    - Declare an integer variable tmpAns.
    - Set tmpAns to DISTANCE['CURRENT_CITY']['CITY'] + GET_MIN_DISTANCE('MASK' | (1 << 'CITY'), 'CITY').
    - Update 'ANS' to min('ANS', tmpAns).
- Return the 'ANS'.

Solve now

02 Approach

In the previous approach, there will be a lot of overlapping subproblems. Hence, we can store results of subproblems by applying memorization to the previous approach and optimize it.

The algorithm is:

Declare a function ‘GET_MIN_DISTANCE’ with parameters ‘MASK’, ‘CURRENT_CITY’, and a 2D array DP[][] (of size (2^N)*N, initially all set as -1), where ‘MASK’ stores the information of the cities that are currently visited,’CURRENT_CITY’ denoted city from where we want to calculate the shortest route and DP[MASK][CURRENT_CITY] stores the minimum distance to reach ‘CURRENT_CITY’ with set bits of ‘MASK’ denoting the cities visited till now.
- If the ‘MASK’ is equal to (1 << N) - 1.
  - Return DISTANCE[CURRENT_CITY][0], since we have fixed city 0 and now we just need to return the cost of the path ‘CURRENT_CITY’ -> 0.
- If DP[MASK][CURRENT_CITY] != -1, since we have visited states before and the results are already cached in DP[MASK][CURRENT_CITY].
  - Return DP[MASK][CURRENT_CITY]
- Declare an integer variable ‘ANS’ and set it to INFINITY.
- Iterate from ‘CITY’ = 0 to ‘N - 1’,
  - If the MASK & (1 << city) == 0, i.e the city-th bit is unset in MASK and this city is unvisited.
    - Declare an integer variable 'TMP_ANS'.
    - Set 'TMP_ANS' to DISTANCE[CURRENT_CITY][CITY] + GET_MIN_DISTANCE(MASK | (1 << CITY), CITY).
    - Update ANS to min(ANS, 'TMP_ANS').
- Return DP[MASK][CURRENT_CITY] = ANS.

Solve now