Encode N-ary tree to binary tree.

You have been given an N-ary tree ‘N’ nodes with node ‘1’ as head of the tree. Encode the above N-ary tree into a binary tree such that if only the encoded binary tree was given to you, you could restore the N-ary tree from the encoded binary tree. You also need to write a function that could decode a given binary tree and return a N-ary tree as in input format.

Note:

There is no restriction on how you encode/decode the N-ary tree.

Example:

N-ary Tree is given as follows:-
6
1 -1 2 3 4 -1 5 -1 6 -1 -1 -1 -1
The above N-ary tree and its encoded binary tree can be represented as follows:-

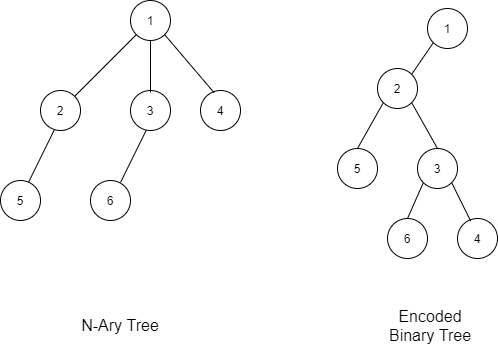
The above binary tree can be represented as follows in their level order traversal:-
1
2 -1
5 3
-1 -1 6 4
-1 -1 -1 -1

Input Format:

The first line contains a single integer ‘T’ representing the number of test cases.

The first line of input contains the elements of the tree in the level order form separated by a single space.

Note:

N-ary Tree is represented in their level order traversal. Each group of children is separated by -1.

Example:

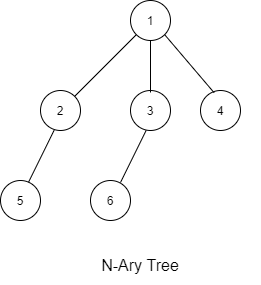
1 -1
2 3 4 -1
5 -1 6 -1 -1
-1 -1

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 -1 2 3 4 -1 5 -1 6 -1 -1 -1 -1

Output Format:

For each test case, for Encode function/method: return the binary tree. For Decode function/method: return the N-ary tree

Note:

1. The list/array storing binary tree must contain ‘N' + 1 element as nodes are numbered from 1 to ‘N’. The 'i'th element of the list/array must contain first the left child then the right child.

2. If a node does not have a left/right child just display that child as -1.

3. You do not need to print anything; it has already been taken care of. Just implement the function.

Constraints:

1 <= T <= 10
1 <= N <= 1000

Time Limit: 1 sec