Last Updated: 11 Dec, 2020

Is Height Balanced Binary Tree

Moderate

Asked in companies

Solve now

Problem statement

You are given the root node of a binary tree.

Return 'true' if it is a height balanced binary tree.

Note:

Height of a tree is the maximum number of nodes in a path from the node to the leaf node.

An empty tree is a height-balanced tree. A non-empty binary tree is a height-balanced binary tree if
1. The left subtree of a binary tree is already the height-balanced tree.
2. The right subtree of a binary tree is also the height-balanced tree.
3. The difference between heights of left subtree and right subtree must not more than ‘1’.

Example:

Input: Consider the binary tree given below:

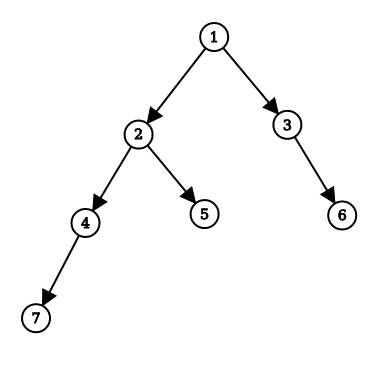
alt text

Output: 'true'

Explanation:
Consider subtree at Node ( 7 ) 
Left subtree height is ‘0’ and right subtree height is ‘0’, the absolute height difference is ‘0-0 = 0’ and ‘0’ is not more than ‘1’ so subtree at Node ( 7 ) is a height-balanced binary tree. 
Same for subtrees at Nodes ( 5, 6 ). 

Consider subtree at Node ( 4 ) 
Left subtree height is ‘1’ and right subtree height is ‘0’, the absolute height difference is ‘1-0 = 1’ and ‘1’ is not more than ‘1’ so subtree at Node ( 4 ) is a height-balanced binary tree.
Same for subtree at Node ( 3)

Consider subtree at Node ( 2 ) 
Left subtree height is ‘2’ and right subtree height is ‘1’, the absolute height difference is ‘2-1 = 1’ and ‘1’ is not more than ‘1’ so subtree at Node ( 2 ) is a height-balanced binary tree.

Consider subtree at Node ( 1 ) 
Left subtree height is ‘3’ and right subtree height is ‘2’, the absolute height difference is ‘3-2 = 1’ and ‘1’ is not more than ‘1’ so subtree at Node ( 1 ) is a height-balanced binary tree.

Because the root node ( 1 ) is a height-balanced binary tree, so the complete tree is height-balanced.

Input Format:

The only line contains elements in the level order form. The line consists of values of nodes separated by a single space. In case a node is null, we take -1 in its place.

For example, the input for the tree depicted in the below image will be:

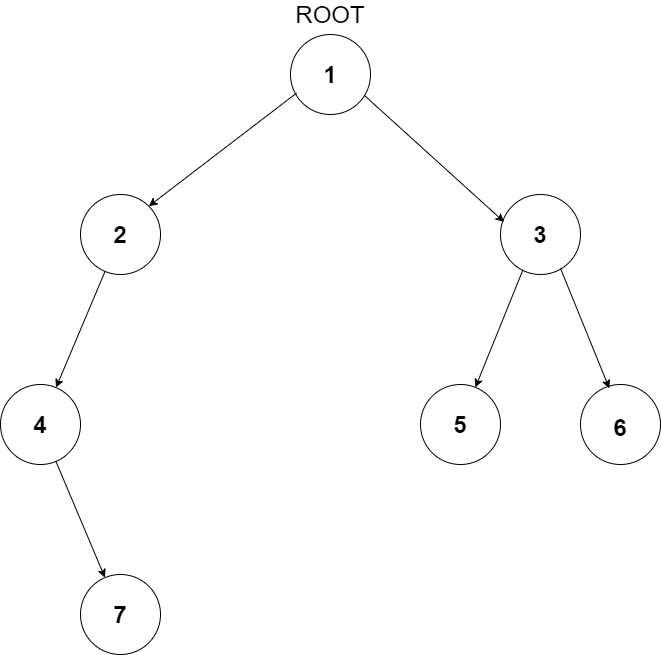
alt text

1
2 3
4 -1 5 6
-1 7 -1 -1 -1 -1
-1 -1

Explanation :
Level 1 :
The root node of the tree is 1

Level 2 :
Left child of 1 = 2
Right child of 1 = 3

Level 3 :
Left child of 2 = 4
Right child of 2 = null (-1)
Left child of 3 = 5
Right child of 3 = 6

Level 4 :
Left child of 4 = null (-1)
Right child of 4 = 7
Left child of 5 = null (-1)
Right child of 5 = null (-1)
Left child of 6 = null (-1)
Right child of 6 = null (-1)

Level 5 :
Left child of 7 = null (-1)
Right child of 7 = null (-1)

The first not-null node(of the previous level) is treated as the parent of the first two nodes of the current level. The second not-null node (of the previous level) is treated as the parent node for the next two nodes of the current level and so on.

The input ends when all nodes at the last level are null(-1).

The sequence will be put together in a single line separated by a single space. Hence, for the above-depicted tree, the input will be given as:

1 2 3 4 -1 5 6 -1 7 -1 -1 -1 -1 -1 -1

Output Format:

Return 'true' or 'false' as stated in the problem statement.

Note :

You do not need to print anything; it has already been taken care of. Just implement the given function.

Solve now

Approaches

01 Approach

The basic idea is that, check for every subtree the current subtree is height-balanced or not

If the subtree is height-balanced then check for its parent subtree. So we need to check the height of the current subtree’s left and right and check the left subtree and right subtree’s height-balanced.

To implement this approach we need to make sure two thing
- The height difference of the left child subtree and the right child subtree must not more than ‘1’.
- Left child subtree and right child subtree must be already balanced.
In height function -
- We implement a height function in which we return the height of a given node
- Suppose given node is ‘currentNode’ than we first find the height of left child subtree height ‘currentNode->left’ and right child subtree height ‘currentNode->right’
- Return max of (currentNode->left, currentNode-> right) +1 , we are extra ‘1’ because ‘+1’ denotes height of current Node in its both children subtrees.
- If ‘currentNode’ has no left child and right child then return ‘1’.
In ‘balancedBinaryTree’ method -
- In this function, we check if the given node’s subtree is height-balanced or not.
- To check the given subtree’s height balancing -
- The first check height difference of both left child subtree and right child subtree height is not more than ‘1’ and left subtree and right subtree both are height-balanced, to check height we use height function which we have already implemented
  - If both conditions are true then return true else return false.

Solve now

02 Approach

The basic idea is to compute height while calling a recursive function. To check if subtrees are balanced or not. So we do some changes in the previous approach, in which we were calling the height function for every node and at the returning time, we were returning ‘true’ if the current subtree is balanced otherwise returning ‘false’. But in this approach, we return the height of the current subtree/node. if we have to return ‘true’ then we return the height of the current subtree/node and if we have to return ‘false’ then return ‘-1’.

In ‘helperMethod’ function -
- In this function, we check if the given node’s subtree is a height-balanced binary tree or not.
- To check if the given subtree is a height-balanced tree or not
- Firstly to check, if the current subtree/node ‘currentNode’ is balanced, we call a recursive function for left subtree ‘currentNode->left’ and right subtree ‘currentNode->right’ and we get two integer values from ‘left’ and ‘right’ child which represent the height of left and right subtree. If the returned value is not ‘-1’ then the respective subtree is balanced otherwise respective subtree is unbalanced.
  - ‘leftValue’ = call recursive function for ‘currentNode->left’.
  - ‘rightValue’ = call recursive function for ‘currentNode->right’.
  - By these two recursive we get two integer values if one of them is ‘-1’, it’s mean either ‘left’ subtree or ‘right’ subtree is not balanced so respective subtree return ‘-1’ as the height of subtree
    - Then we return ‘-1’ because if the child node/subtree is not balanced then the parent node can’t be balanced.
  - If both values ‘leftValue’ and ‘rightValue’ are not ‘-1’ and the absolute difference between them is not more than 1 then return a max of ( ‘leftValue’, ‘rightValue’ )+1.
The above step is done in ‘helperMethod’, in the main method, ‘helperMethod’ will return an integer
- If the return value is not ‘-1’ then return ‘True’ because the root node or tree is balanced.
- Otherwise, return ‘False’.

Solve now