Last Updated: 1 Oct, 2021
LCA - Lowest Common Ancestor
Hard
Asked in companies



The lowest common ancestor (LCA) is a concept in graph theory and computer science.
Let ‘T’ be a rooted tree with ‘N’ nodes. The lowest common ancestor is defined between two nodes, ‘u’ and ‘v’, as the lowest node in ‘T’ that has both ‘u’ and ‘v’ as descendants (where we allow a node to be a descendant of itself). - Wikipedia
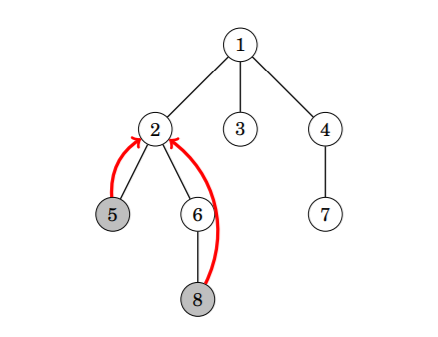
For the given tree, The LCA of nodes 5 and 8 will be node 2, as node 2 is the first node that lies in the path from node 5 to root node 1 and from node 8 to root node 1.
Path from node 5 to root node looks like 5 → 2 → 1.
Path from node 8 to root node looks like 8 → 6 → 2 → 1.
Since 2 is the first node that lies in both paths. Hence LCA will be 2.
Given any two nodes ‘u’ and ‘v’, find the LCA for the two nodes in the given Tree ‘T’.
Note: For each test case, the tree is rooted at node 1.
Input Format-
The first line contains an integer ‘T’ which denotes the number of test cases.
For each test case:
The first line contains a single integer ‘N’, denoting the number of nodes.
Each of the following ‘N’ - 1 line contains two space-separated integers, ‘ui’ and ‘vi’, which means an edge connects these two nodes.
The following line will contain a single integer ‘Q’, denoting the number of queries you have to answer for the given tree.
In the following ‘Q’ lines, each one will have two numbers, ‘u’ and ‘v’, for which you have to find the LCA of ‘u’ and ‘v’.
Output Format-
Your task is to print ‘Q’ lines for each test case.
The ‘Q’ lines should be the LCA of the given ‘u’ and ‘v’, respectively.
Constraints -
1<= ‘T' <= 5
1 <= ‘N’ <= 10^5
1 <= ‘Q’ <= 10^5.
1 <= ‘u’, ‘v’ <= ‘N’.
Time Limit: 1 sec
Approaches
Prerequisite - DFS
Approach:
We will store the depth and the direct parent of each node using a dfs.
Now, if we have to find the LCA to two nodes, first we would move upward the node which has a higher depth until both the nodes reach the same depth, then we will move both the node upward until they become the same, the node that we reach will be the LCA.
Algorithm:
- Initialize two arrays of length ‘N + 1’ to store depth and the direct parent of each node.
- Func dfs(cur, parent):
- Update depth[cur] to depth[parent] + 1.
- Update par[cur] to parent
- Iterate in all the children of node ‘cur’ and call dfs as dfs(child, cur)
- Func get_lca(u, v):
- While depth[u] > depth[v]:
- Update u to par[u]
- While depth[v] > depth[u]:
- Update v to par[v]
- While u != v:
- Update u to par[u]
- Update v to par[v]
- Return u
- While depth[u] > depth[v]:
- Func Main():
- dfs(1, 0)
- For u,v in query:
- print(get_lca(u, v))
Prerequisite - Sparse Table, DFS
Approach:
Using Sparse Table, we can efficiently find the kth ancestor of any node in the tree in O(log(N)). Using this, we can divide the problem of finding the LCA into two parts. We use two pointers that initially point to the two nodes whose LCA we have to find.
Let’s take an example:
We have to find the LCA of nodes ‘4’ and ‘5’.
The black circle around the nodes denote the current positions of both the pointers.
Initially, both point to initial nodes which are node ‘4’ and node ‘5’.
Now, one of the pointers moves upwards so that both pointers point to nodes at the same level. I.e. we will move our pointer upward, which has a higher depth until both of the pointers reach the same depth. This can be done in O(log(N)) by using a sparse table.
After this, we determine the minimum number of steps needed to move both pointers upwards to point to the same node. The node to which the pointers point after this is the lowest common ancestor.
The example suffices to move both pointers one step upwards to node 1, which is the lowest common ancestor.
Algorithm:
Initialize a variable ‘level’ to log(N) + 3;
Initialize a 2d array ‘dp’ of dimension ‘(N + 1) * level’ to find the ‘kth’ ancestor of any tree node using the sparse table technique.
Initialize an array ‘depth’ of length ‘N + 1’ to store the depth of all the nodes from root node 1.
- Func dfs(curr, par)
- Update dp[cur][0] to par.
- Update depth[cur] to depth[par] + 1.
- Run a for loop from i = ‘1’ to ‘level’. → standard filling of a sparse table
- If dp[cur][i - 1] is not ‘0’.
- Update dp[cur][i] to dp[dp[cur][i - 1]][i -1].
- If dp[cur][i - 1] is not ‘0’.
- Iterate in all the children of node ‘cur’ and call dfs as dfs(child, cur)
- Func get_lca(u, v):
- Swap ‘u’ and ‘v’ if the depth of node ‘u’ is greater than node ‘v.’,I.e. if depth[u] > depth[v] swap(u, v)
- Initilaze a variable dis equals to depth[v] - depth[u].
- Run a for loop from i = ‘0’ to ‘level’. → making both the nodes at the same depth.
- If ‘ith’ bit in ‘dis’ is set i.e. d & (1 << i) == 1.
- Update ‘v’ to dp[v][i]
- If ‘ith’ bit in ‘dis’ is set i.e. d & (1 << i) == 1.
- If node ‘u’ and ‘v’ are the same, return ‘u’ as we have found the LCA.
- Run a for loop from i = ‘level - 1’ to ‘0’.
- If (2 ^ i)th parent of ‘u’ and ‘v’ is same, i.e. dp[u][i] == dp[v][i],
- We do nothing
- Else
- We update ‘u’ to dp[u][i]
- We update ‘v’ to dp[v][i]
- If (2 ^ i)th parent of ‘u’ and ‘v’ is same, i.e. dp[u][i] == dp[v][i],
- We return parent of ‘u’, i.e. dp[u][0].
Func Main():
- dfs(1, 0)
- For each query
- Print get_lca(u, v)

