Last Updated: 16 Dec, 2020
M-Coloring Problem
Moderate
Asked in companies



You are given an undirected graph as an adjacency matrix consisting of 'v' vertices and an integer 'm'.
You need to return 'YES' if you can color the graph using at most 'm' colors so that no two adjacent vertices are the same. Else, return 'NO'.
For example:
Input:
If the given adjacency matrix is:
[0 1 0]
[1 0 1]
[0 1 0] and 'm' = 3.
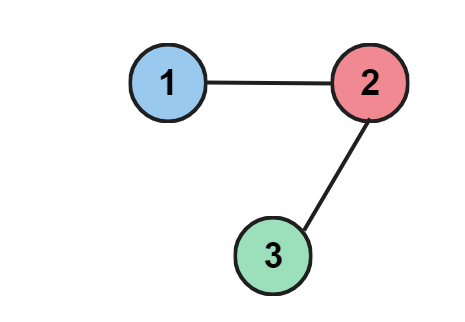
Output: YES
Explanation:
The given adjacency matrix tells us that 1 is connected to 2 and 2 is connected to 3. We can use three different colors and color all three nodes.
Hence we return true.
Input Format:
The first line contains two space-separated integers, 'v' and 'm', denoting the number of vertices in the undirected graph and the number of colors, respectively.
Each of the next 'v' lines contains 'v' integers denoting the adjacency matrix of the undirected graph.
Output Format:
You need to return “YES” if we can color the graph with at most M colors. Otherwise, return “NO”. (without the inverted commas)
Note:
You are not required to print the expected output. It has already been taken care of. Just implement the function.
Approaches
- We generate all possible combinations of colors possible for coloring the given graph.
- This can be done recursively by assigning a node each color from 1 to M and doing the same for all nodes.
- We further check if the adjacent vertices don’t have the same color.
- If we find such a combination of vertices, we return “YES”. Otherwise, we return “NO”.
- We generate all possible combinations of colors possible for coloring the given graph.
- An optimization in this method would be assigning the colors after checking if making the vertex of that color is possible. We check this in the brute force method after assigning all the colors.
- We would assign each vertex a color from 1 to M and check if its adjacent vertex has a different color.
- Finally, if we get a configuration such that each node is colored from 1 to M and adjacent vertices are of different colors, we return “YES”. Otherwise, we return “NO”.
Similar problems

