Introduction
In this blog, we will understand a very interesting problem of a Binary Search Tree data structure. We have already learned that there are three ways in which we can traverse a tree. These are, namely, preorder, inorder, and postorder. In this problem, we will print leaf nodes from the preorder of a BST.

Through this problem, we will learn the approach to solve any such problem of a Binary Search Tree. Firstly, we will examine the problem statement, learn about the Binary Search tree data structure, and decide on what will be the optimum approach. Then we will proceed toward the implementation in the programming languages.

What is a Binary Search Tree?
A Binary Search Tree is a type of Binary tree data structure. A Binary Tree is one in which elements have the utmost two children nodes. Since elements in this data structure have only two child nodes, we name them the left child and the right child. Any node of Binary contains the following information. These are its data and pointers to its left and right child.
For Example, if we consider the tree below, 20 is the root node, and the rest of the nodes are its children nodes. We pick any node, say 17, so 13 will be its left child, and 19 will be its right child. 17 is the parent node to children nodes 13 and 19.

Three properties of a Binary Search Tree that differentiates it from a normal Binary Tree. These properties are mentioned below in the list.
- The left subtree of any node will contain only those whose value is lesser than that node’s value.
- The right subtree of any node will contain only those whose value is greater than that node’s value.
- All the subtrees must also be binary search trees.
Problem Statement
We are given a preorder of a binary search tree with n nodes. We have to find and print leaf nodes from the preorder of a BST. There may be any number of leaf nodes in the BST.
Here, we assume that all the nodes’ values are positive. Let us understand this with the help of an example.
Suppose we have a BST preordered, as seen in the examples below. We have to print leaf nodes from them. We will use multiple examples so that you can get a better understanding of the problem statement.
Sample Examples
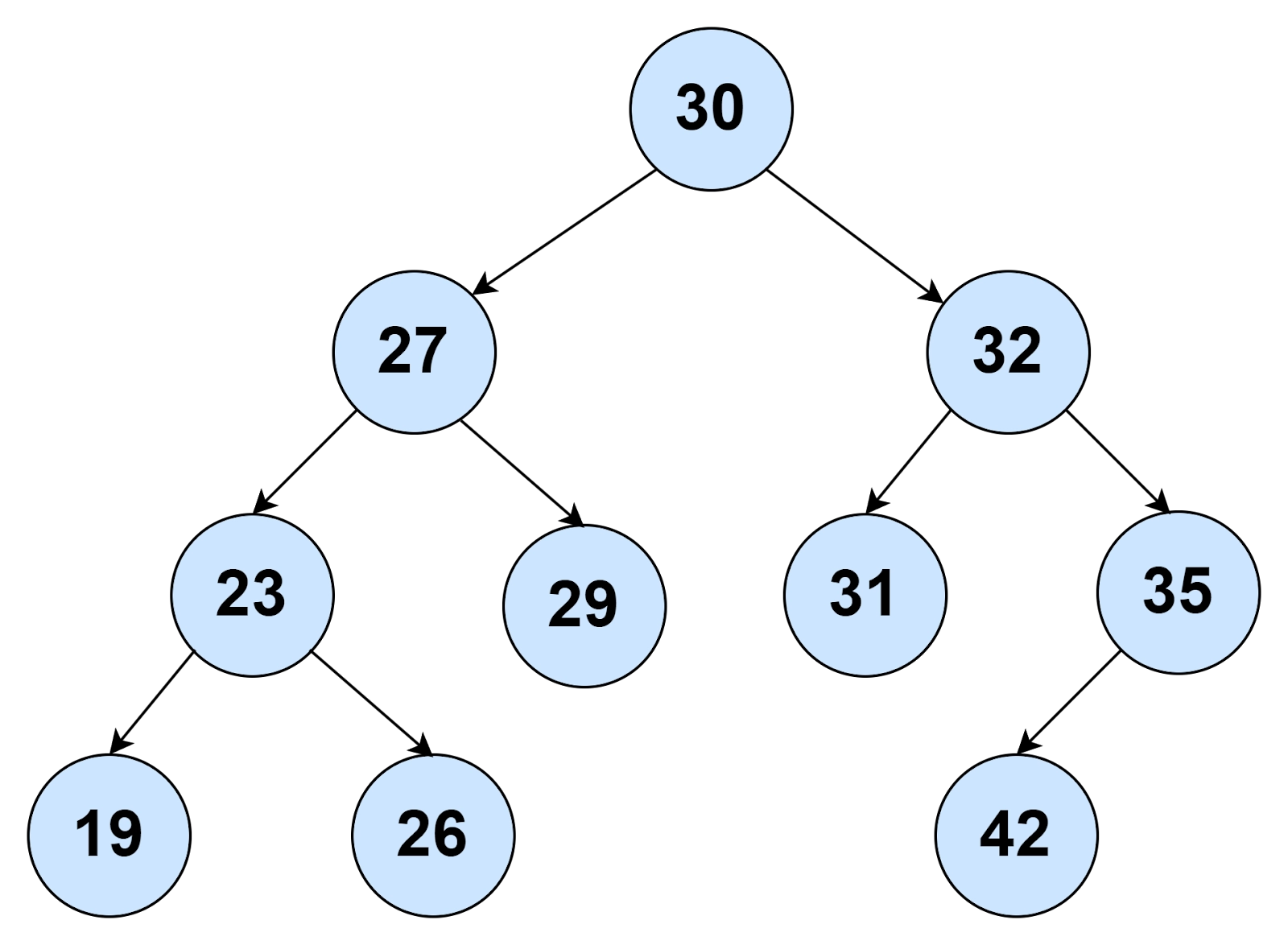
🌷 Example 1:
|
Input: 30 27 23 19 26 29 32 31 35 42 Output: 19 26 29 31 42 |
Explanation
In the above example, we can see a preorder of a binary search tree. Using the given preorder, we will output the leaf nodes of that BST. If you are familiar with the basic terminologies of the tree, this problem will not be difficult for you.
You might know that preorder traversal goes from root to left subtree and then to right subtree.
- In the given preorder, observe the decreasing order from 30 to 19.
- This decreasing order breaks when we get 26. As a result, 19 is pushed onto the stack.
- The same happens for 26 and 29. They are pushed to the stack because the value ahead of them is greater.
- 32 is not pushed because the consecutive value is less.
- We check that 32 is greater than the top of the stack. If this case is true, we will pop the stack. 19 will be printed as a result.
This way, the process continues, and every leaf node value will be popped out of the stack. You can use the BST created using the preorder for a better grab.
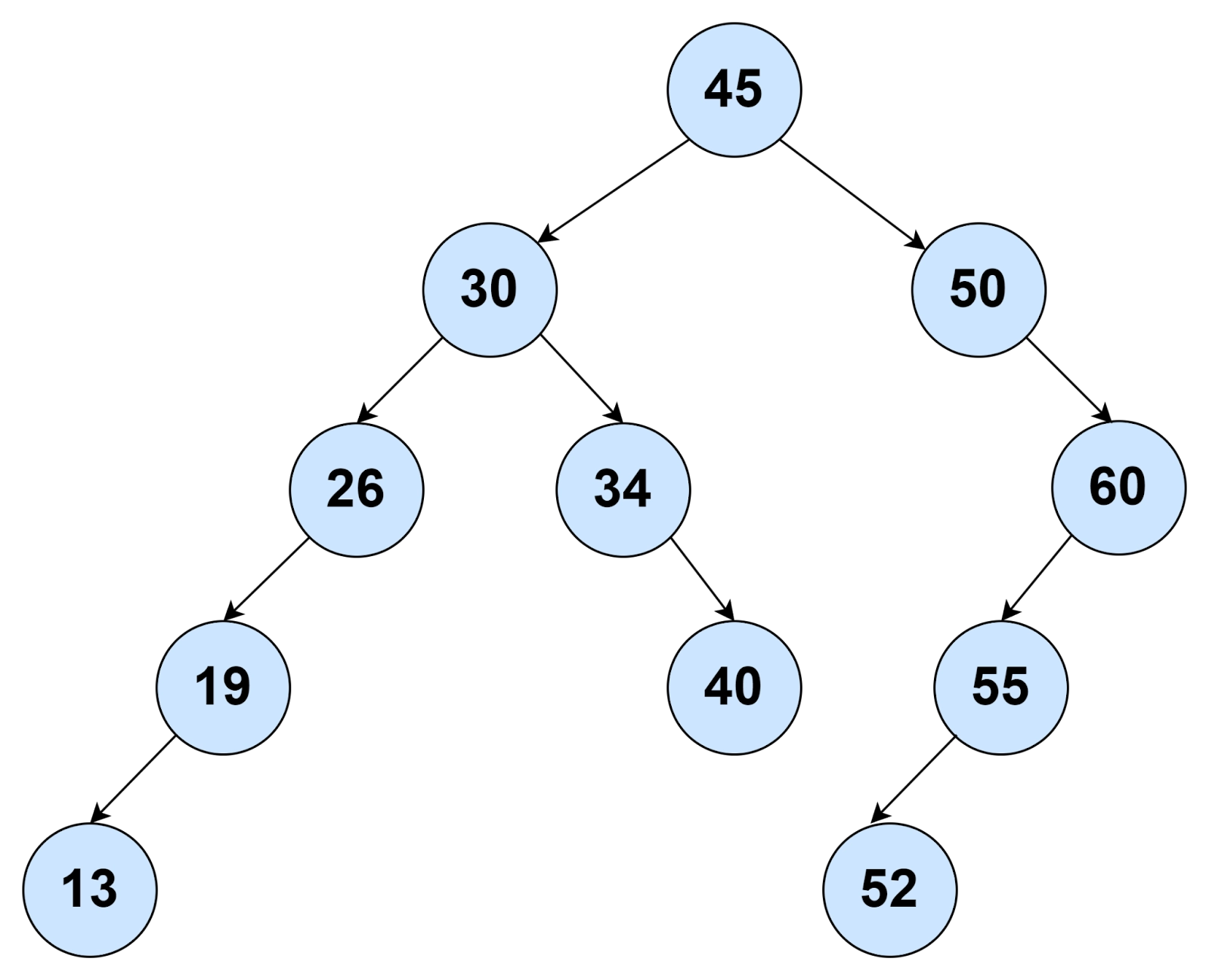
🌷 Example 2
|
Input: 45 30 26 19 13 34 40 50 60 55 52 Output: 13 40 52 |
Explanation
- In the given preorder, observe the decreasing order from 45 to 13.
- This decreasing order breaks when we get 34. As a result, 13 is pushed onto the stack.
- The same happens for 34, 40, 50, and 52. They are pushed to the stack because the value ahead of them is greater.
- 55 is not pushed because the consecutive value is less.
- We check if 34 is greater than the top of the stack. If this case is true, we will pop the stack. 13 will be printed as a result.
This way, the process continues, and every leaf node value will be popped out of the stack one by one. You can use the BST created using the preorder for a better grab.
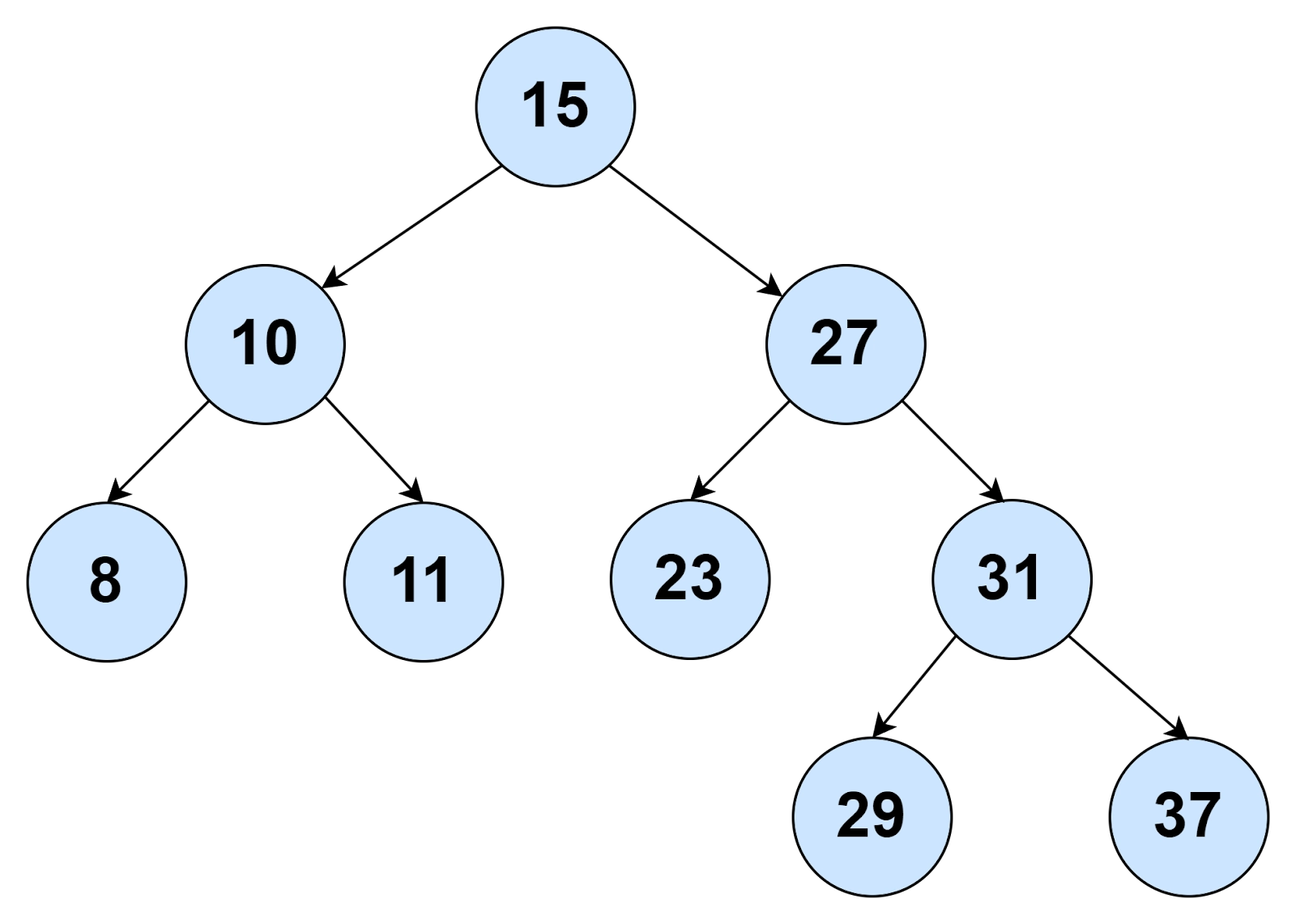
🌷 Example 3
|
Input: 15 10 8 11 27 23 31 29 37 Output: 8 11 23 29 37 |
Explanation
- In the given preorder, observe the decreasing order from 15 to 8.
- This decreasing order breaks when we get 11. As a result, 8 is pushed onto the stack.
- The same happens for 11, 23, 29, and 37. They are pushed to the stack because the value ahead of them is greater.
- 27 is not pushed because the consecutive value is less.
- We check that 11 is greater than the top of the stack. If this case is true, we will pop the stack. 8 will be printed as a result.
This way, the process continues, and every leaf node value will be popped out of the stack. You can use the BST created using the preorder for a better grab.