Check whether a given Binary Tree is Complete or not

Introduction 

This article will discuss the problem of whether a binary tree is complete or not; before reading the problem statement, let's first discuss in brief what is a complete binary tree.

A complete binary tree is a binary tree in which every level, except the last one, is completely filled, and all nodes are leftmost as possible. 

Let us see the below examples for better understanding:

A complete binary tree

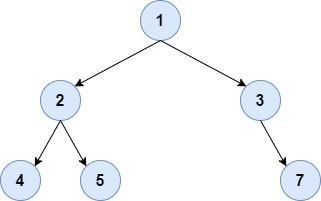
An incomplete binary tree

Problem Statement

We are given a Binary Tree. Write a program to check whether the given Binary Tree is a Complete Binary Tree or not.

Sample Examples

Input 1:

      1
    /    \
   2      3
  /  \    /
 4    5  6 

Output 1:

 True

Explanation: Since every level, except possibly the last, is completely filled, and all nodes are as far left as possible, so the given tree is complete.

Input 2:

      1
    /    \
   2      3
         /  \
        4    5

Output 2:  

False

Explanation: Since all nodes are not as far left as possible, so the given tree is not complete.

Level order traversal approach

We can use the modified level order traversal to check whether a given binary tree is complete or not. To understand the approach, let us first understand the term ‘Full Node’. ‘Full Node’ is a node if both left and right children are not empty (or not NULL). 

The idea is to do a level order traversal starting from the root. If a node is NOT a full node, then all the remaining nodes in the queue should not have any children.

Also, we need to check one more thing to handle the below case: If a node has a left empty child, then the right child must be empty.   

Algorithm

1. Create an empty queue and enqueue the root node.
2. Use a flag variable of boolean type to mark the end of full nodes.
3. Loop till the queue is empty.
4. Dequeue front node.
5. If we encounter a non-full node before and the current node is not a leaf then a tree cannot be complete. So, return false.
6. If the left child is empty but the right child exists then also a tree cannot be complete. Return false.
7. If the left child exists, enqueue it else if the current node is a non-full node, set the flag to true.
8. If the right child exists, enqueue it else if the current node is a non-full node, set the flag to true.
9. End the loop.

Code In Java

import java.util.LinkedList;
import java.util.Queue;

public class CompleteBTree
{
	static class Node
	{
		int data;
		Node left;
		Node right;
		
		// Constructor
		Node(int d)
		{
			data = d;
			left = null;
			right = null;
		}
	}

	static boolean isCompleteBT(Node root)
	{
		// Base Case
		if(root == null)
			return true;
		
		// Create an empty queue
		Queue<Node> queue =new LinkedList<>();
		
		boolean flag = false;
		
		queue.add(root);
		while(!queue.isEmpty())
		{
			Node temp_node = queue.remove();
			
			/* Check if left child is present*/
			if(temp_node.left != null)
			{
					if(flag == true)
					return false;
				
				// Enqueue Left Child
				queue.add(temp_node.left);
			}
			// If this a non-full node, set the flag as true
			else
				flag = true;
			
			/* Check if right child is present*/
			if(temp_node.right != null)
			{
				if(flag == true)
					return false;
				
				// Enqueue Right Child
				queue.add(temp_node.right);
				
			}
			// If this a non-full node, set the flag as true
			else
				flag = true;
		}
		// If we reach here, then the tree is complete Binary Tree
		return true;
	}

	public static void main(String[] args)
	{
	 Node data = new Node(1);
        data.left = new Node(2);
        data.right = new Node(3);
        data.left.left = new Node(4);
        data.left.right = new Node(5);
        data.right.left = new Node(6);
        data.right.right = new Node(7);
		
		if(isCompleteBT(data) == true)
			System.out.println("Complete Binary Tree");
		else
			System.out.println("NOT Complete Binary Tree");
	}

}

You can also try this code with Online Java Compiler

Run Code

Output: 

Complete binary tree

You can also try this code with Online Java Compiler

Run Code

Code In C++

#include <iostream>
#include <list>
using namespace std;
 
struct Node
{
    int key;
    Node *left, *right;
 
    Node(int key)
    {
        this->key = key;
        this->left = this->right = nullptr;
    }
};
 
bool isComplete(Node* root)
{
      if (root == nullptr) {
        return true;
    }
 
    list<Node*> queue;
    queue.push_back(root);
 
    Node* front = nullptr;
 
    bool flag = false;
    while (queue.size())
    {
        // dequeue front node
        front = queue.front();
        queue.pop_front();
 
        // if we have encountered a non-full node before and the current   //node is not a leaf, a tree cannot be complete
        if (flag && (front->left || front->right)) {
            return false;
        }
 
        // if the left child is empty and the right child exists,
        // a tree cannot be complete
        if (front->left == nullptr && front->right) {
            return false;
        }
 
        // if the left child exists, enqueue it
        if (front->left) {
            queue.push_back(front->left);
        }
        // if the current node is a non-full node, set the flag to true
        else {
            flag = true;
        }
 
 
        // if the right child exists, enqueue it
        if (front->right) {
            queue.push_back(front->right);
        }
        // if the current node is a non-full node, set the flag to true
        else {
            flag = true;
        }
    }
 
    return true;
}
 
int main()
{         
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->left = new Node(6);
    root->right->right = new Node(7);
 
    if (isComplete(root)) {
        cout << "Complete binary tree";
    }
    else {
        cout << "Not a complete binary tree";
    }
 
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output: 

Complete binary tree

Complexity Analysis

Time complexity: O(n); where n is the number of nodes in the Binary Tree.

Space Complexity: O(n) due to the usage of the queue.