Algorithm
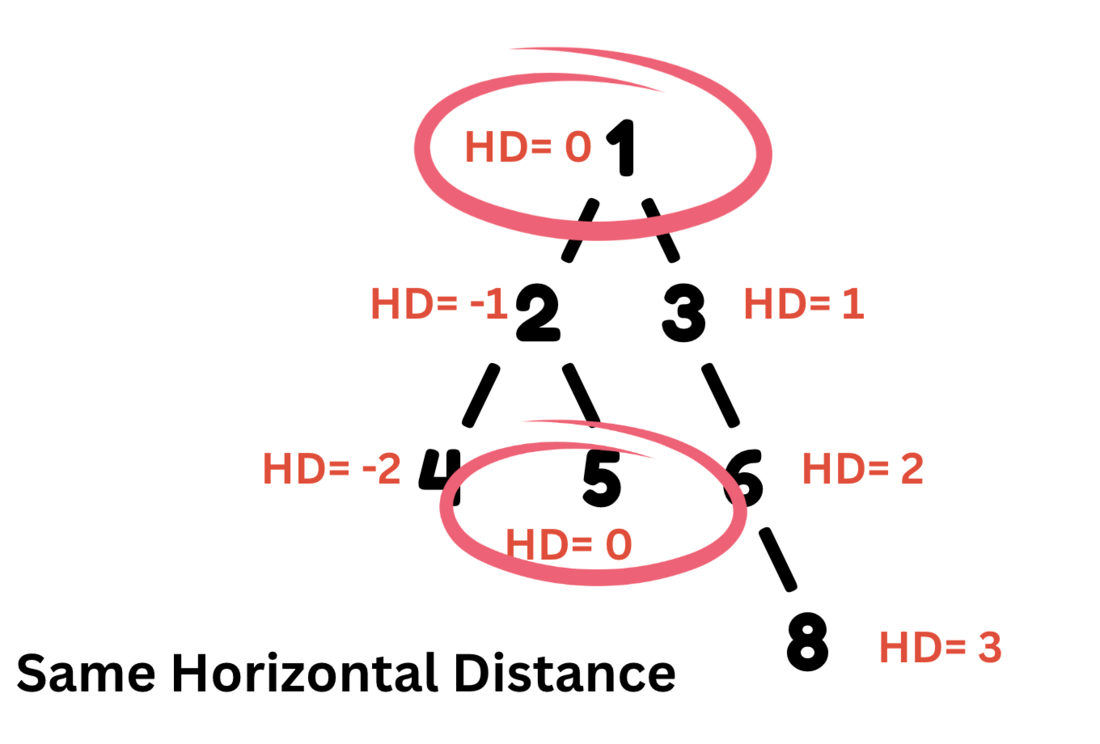
The algorithm works by traversing the binary tree and mapping all the nodes on the same vertical line to the horizontal distance. It then compresses the nodes on each vertical line by counting the number of set bits and clear bits at each bit position and setting the corresponding bit of the compressed node.
Below are the steps that we can follow to solve the problem:
-
We start by defining a binary tree using the Node class, which has a value (val) and left and right pointers (left, right) that point to the left and right subtrees, respectively.
-
We then define a function BTraversal that recursively traverses the binary tree and maps all the nodes of the same vertical line to the horizontal distance using a map. The map is used to store the nodes for each horizontal distance, where the horizontal distance is defined as the distance of the node from the root node in terms of the number of left or right turns.
-
We define a utility function evaluateComp, that compresses all the nodes on the same vertical line with a single node that satisfies a condition. This function takes a vector arr as input, which contains all the nodes on the same vertical line.
-
To compress the nodes, we iterate over the range of bit positions from 0 to 31.
For each bit position i, we count the number of set bits and clear bits at that position for all the nodes in the vector arr.
If the count of set bits is greater than the count of clear bits, we set the ith bit of the compressed node to 1.
Otherwise, we set the ith bit of the compressed node to 0.
-
We then define the compressBTree function that uses the BTraversal function to map all the nodes on the same vertical line and the evaluateComp function to compress the nodes on each vertical line.
-
Finally, we create a binary tree and call the compressBTree function to compress the nodes on each vertical line.
Let us look at the implementation of the above algorithm and let us find out the complexity analysis.
Code in C++
/* C++ program for
Compress a Binary Tree
Based on an Overlapping Condition */
#include <bits/stdc++.h>
using namespace std;
/* defining the structure of a node of the tree */
class Node {
public: int val;
/* define pointers for
left and right subtrees */
Node * left,
* right;
Node(int val) {
this -> val = val;
left = right = NULL;
}
};
/* Utility Function to compress all the nodes on the same vertical line */
void evaluateComp(vector < int > & arr) {
/* store node by compressing all nodes on the current
vertical line */
int result = 0;
// to check if ith bit of current number set or not
int getBit = 1;
// Iterate over the range [0, 31]
for (int i = 0; i < 32; i++) {
// store count of set bits at ith positions
int SB = 0;
// store count of clear bits at ith positions
int CB = 0;
// loop to count the number of set and clear bits
for (auto j: arr) {
// If ith bit of current element is set
if (getBit & j)
SB++; // Update SB
else
CB++; // Update CB
}
/* If the count of set bits at ith position is greater
than count of clear bits, then
set the resultant bit as set */
if (SB > CB)
// Update result by setting the ith bit
result += pow(2, i);
// Update getBit
getBit <<= 1;
}
cout << result << " ";
}
/* Function to traverse the tree and map all the nodes of
same vertical line to horizontal distance */
void BTraversal(Node * root, int hd, map < int, vector < int > > & mp) {
if (!root)
return;
// Storing the values in the map
mp[hd].push_back(root -> val);
// Recursive calls on left and right subtree
BTraversal(root -> left, hd - 1, mp);
BTraversal(root -> right, hd + 1, mp);
}
/* Function to compress all the nodes on the same vertical
line with a single node that satisfies the condition */
void compressBTree(Node * root) {
// Map all the nodes on the same vertical line
map < int, vector < int > > mp;
BTraversal(root, 0, mp);
// Getting the range of horizontal distances
int lower, upper;
for (auto i: mp) {
lower = min(lower, i.first);
upper = max(upper, i.first);
}
for (int i = lower; i <= upper; i++)
evaluateComp(mp[i]);
}
// Driver Code
int main() {
Node * root = new Node(1);
root -> left = new Node(2);
root -> right = new Node(3);
root -> left -> left = new Node(4);
root -> left -> right = new Node(5);
root -> right -> right = new Node(6);
root -> right -> right -> right = new Node(8);
// Function Call
compressBTree(root);
return 0;
}

You can also try this code with Online C++ Compiler
Code in Java
import java.util.*;
// Structure of a node of the tree
class Node {
int val;
Node left, right;
Node(int val) {
this.val = val;
left = right = null;
}
}
// Class to store the compressed node and its count
class CompressedNode {
int node;
int count;
CompressedNode(int node, int count) {
this.node = node;
this.count = count;
}
}
// Main class
class BinaryTreeCompression {
/* Function to compress the nodes with a single node
that meets the condition */
static void evaluateComp(List<Integer> arr) {
/* store node by compressing all nodes on the current
vertical line */
int result = 0;
// Check if ith bit of current bit set or not
int getBit = 1;
// Iterate over the range [0, 31]
for (int iter = 0; iter < 32; iter++) {
// store count of set bits at ith positions
int SB = 0;
// store count of clear bits at ith positions
int CB = 0;
// Traverse the array
for (int j : arr) {
// If ith bit of current element is set
if ((getBit & j) != 0)
SB++; // Update SB
else
CB++; // Update CB
}
/* If count of set bits at ith position is greater
than count of clear bits */
if (SB > CB)
// Update result
result += Math.pow(2, iter);
// Update getBit
getBit <<= 1;
}
System.out.print(result + " ");
}
/* Function to traverse the tree and map all the nodes of
same vertical line to horizontal distance */
static void BTraversal(Node root, int hd, Map<Integer, List<Integer>> mp) {
if (root == null)
return;
// Storing the values in the map
List<Integer> values = mp.getOrDefault(hd, new ArrayList<>());
values.add(root.val);
mp.put(hd, values);
// Recursive calls on left and right subtree
BTraversal(root.left, hd - 1, mp);
BTraversal(root.right, hd + 1, mp);
}
// Function to compress the nodes with a single node
static void compressBTree(Node root) {
// Map all the nodes on the same vertical line
Map<Integer, List<Integer>> mp = new HashMap<>();
BTraversal(root, 0, mp);
// Getting the range of horizontal distances
int lower = Integer.MAX_VALUE, upper = Integer.MIN_VALUE;
for (int i : mp.keySet()) {
lower = Math.min(lower, i);
upper = Math.max(upper, i);
}
for (int i = lower; i <= upper; i++) {
evaluateComp(mp.get(i));
}
}
// Driver Code
public static void main(String[] args) {
Node root = new Node(1);
root.left = new Node(2);
root.right = new Node(3);
root.left.left = new Node(4);
root.left.right = new Node(5);
root.right.right = new Node(6);
root.right.right.right = new Node(8);
// Function Call
compressBTree(root);
}
}

You can also try this code with Online Java Compiler
Output
4 2 1 3 6 8
Complexity Analysis
Time Complexity:
O(N log N), where N is the number of nodes in the binary tree.
This is because the function involves a recursive traversal of the entire tree, and for each node, it performs a constant amount of work that involves updating a map and performing bitwise operations.
Space Complexity:
O(N), where N is the number of nodes in the binary tree.
This is because the function uses a HashMap to store the nodes mapped to their respective horizontal distances, and the size of the map can be, at most, N.
Additionally, the function uses a List or vector to store the values in the map, which can also have a maximum size of N.
Therefore, the total space complexity is O(N * N) = O(N2).
Frequently Asked Questions
What is recursion?
Recursion is a programming technique where a function calls itself. This is often used to solve problems that can be broken down into smaller, simpler sub-problems.
Why is Tree called a non-linear data structure?
A tree is called a non-linear data structure because it does not store data in a linear sequence like an array or a linked list. Instead, it organizes data hierarchically, with a parent-child relationship between nodes.
What is the difference between a binary tree and a binary search tree?
A binary tree is a tree where each node has at most two children. On the other hand, a binary search tree is a binary tree where the value of each node is greater than or equal to the values of all the nodes in its left subtree and less than or equal to the values of all the nodes in its right subtree.
Conclusion
To conclude the discussion, we have extensively looked at the problem based on binary trees, i.,e, Compress a Binary Tree Based on an Overlapping Condition. We used mapping to solve the problem. At last, we also looked at the complexity analysis of the approach.
Check out this problem - Connect Nodes At Same Level
On the Coding Ninjas Platform, we have various such problems. Additionally, Coding Ninjas recently introduced the Coding Ninjas Studio Test Series, a mainly developed test series for acing interviews.
Thank you for taking the time to read this. I hope this blog has been helpful to you.