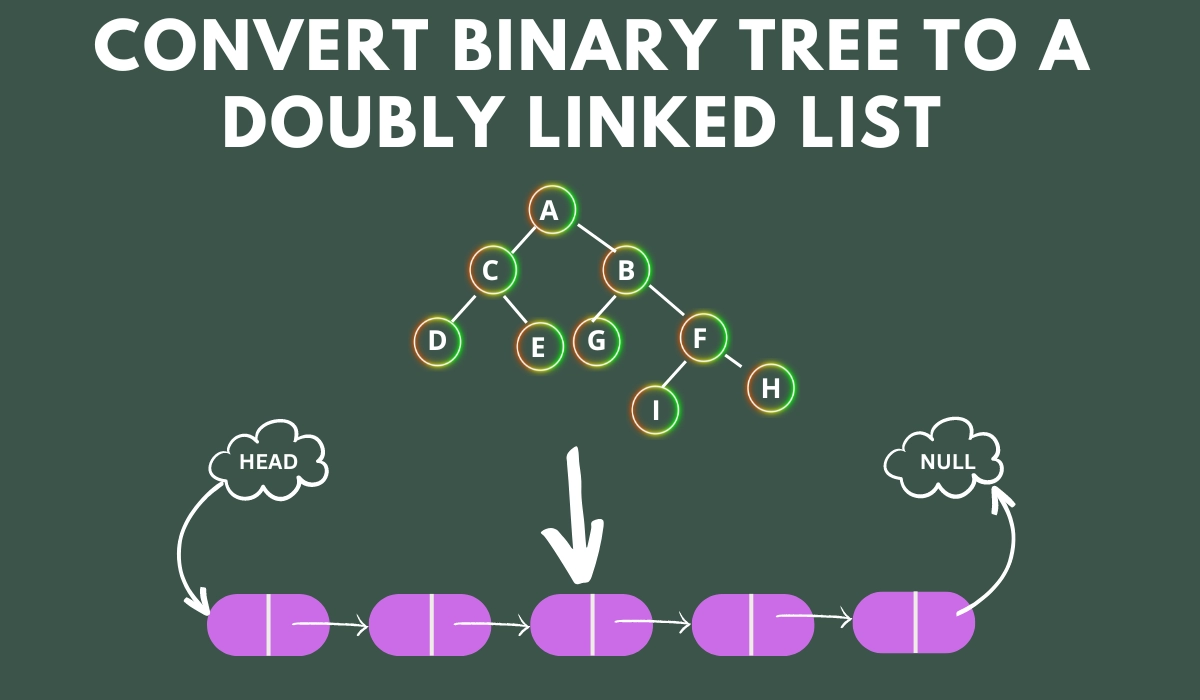
Doubly Linked List

A Doubly Linked List is a linear data structure where each node is connected to its previous and next neighbours. Each node has three attributes, namely the prev containing the address of the last node, the next containing the address of the next node, and data including the node's value.
Problem Statement
Given a Binary Tree. Convert it to a Doubly Linked List, following the inorder Traversal.
E.g., Consider the following tree. The tree is given in breadth-first order.
tree = [ 10, 12, 15, 25, 30, 36 ]
should generate the following doubly linked list,
25 -> 12 -> 30 -> 10 -> 36 -> 15
Sample Examples
Let's check out some examples to get a better picture.
Example 1
Let's take a binary tree to be tree = [ 10, 12, 15, 25, 30, 36 ], and we are supposed to create a doubly linked list from it.
Input
tree = [ 10, 12, 15, 25, 30, 36 ]
You are given the address of the root node of the tree. Note that the above array represents the tree in breadth-first order, and the actual input is the root of the binary tree.
Note: You are not supposed to generate a binary tree from the input.
Output
25 -> 12 -> 30 -> 10 -> 36 -> 15
Return the head pointer (starting node's address) to the doubly linked list.
Example 2
Let's take a binary tree to be tree = [ 10, 20, null, 30, 40, null, null, null, null], and we are supposed to create a doubly linked list from it.
Input
tree = [ 10, 20, null, 30, 40, null, null, null, null ]
You are given the address of the root node of the tree. Note that the above array represents the tree in breadth-first order, and the actual input is the root of the binary tree.
Note: You are not supposed to generate a binary tree from the input.
Output
30 -> 20 -> 40 -> 10
Return the head pointer (starting node's address) to the doubly linked list.
Approach
We will be following the simple brute force approach and doing as said. We will be following the in-order Traversal in the binary tree and generating a node for the linked list as we come across the node of the tree.
For generating the doubly linked list, we shall be following the Insertion to a doubly linked list, and for traversing the tree, we shall be following the inorder Traversal.
Algorithm
Let us look at the algorithm of the above problem.
- Traverse through the binary tree via inorder traversal, i.e recurse through the function via the left child, the node value, and then a right child.
- On reaching the null point, create a node for a doubly linked list, and set its prev and next values to be null, and the data attribute to be the leaf node value.
- Now, on returning to the parent node, we create a new node with this value, set the child’s node next to be the parent, and set the parent’s prev to be the child node.
- Then, on returning from this recursive function we shall be getting a doubly linked list, generated from the binary tree.
Dry Run
Let's look over a dry run for an example to get a better understanding.
Input
tree = [ 10, 12, 15, 25, 30, 36 ]
Step 1: Traverse through the Binary Tree, via inorder traversal, and reach the leaf node.

As we can see, the tree's root node is 10, and we are following in-order Traversal, so we will be iterating until we reach the tree's end.
Step 2: On reaching the leaf node, create a new node of the doubly linked list, with the data attribute set to the leaf node’s value.
Step 3: For every node of a tree, the left child becomes the prev pointer of the doubly linked list node, and the right child becomes the next pointer of the doubly linked list node.

Step 4: Once we reach null, we create a new node for the doubly linked list, its prev being the left child and its next being its right child.
Then on returning via recursion, we assign the prev of the node and re-assign the next of the parent node.

Implementation in Python
class Node:
# definition of node of a doubly linked list
def __init__(self, data: int = -1, next=None, prev=None) -> None:
self.data = data
self.next = next
self.prev = prev
class TreeNode:
# definition of a node of a binary tree
def __init__(self, data: int = -1, left=None, right=None) -> None:
self.data = data
self.left = left
self.right = right
# global variables defining the head pointer
# of doubly linked list
global_head = None
temp = None
def inorder(root: TreeNode) -> None:
# inorder traversal of a tree
if root is None:
return None
inorder(root.left)
# creating a new node for doubly linked list
global global_head
temp_head = Node(root.data)
global temp
# if there is no global head then the leftmost leaf node
# becomes head of doubly linked list
# else we continue to add new nodes to the linked list
if global_head is None:
global_head = temp_head
temp = global_head
else:
temp.next = temp_head
temp_head.prev = temp
temp = temp.next
inorder(root.right)
# driver code
# generating Binary Tree
root = TreeNode(10)
root.left = TreeNode(12)
root.right = TreeNode(15)
root.left.left = TreeNode(25)
root.left.right = TreeNode(30)
root.right.left = TreeNode(36)
# stores the inorder traversal of the binary tree
inorder(root)
# displays the doubly linked list
while global_head:
print(global_head.data, end=" -> ")
global_head = global_head.next
print()
Output

Implementation in C++
#include <bits/stdc++.h>
#define ll long long int
using namespace std;
struct node
{
// definition of the node of doubly linked list
int data;
node *next;
node *prev;
node(int data)
{
// constructor for creating a node of doubly linked list
this->data = data;
this->next = NULL;
this->prev = NULL;
}
};
struct TreeNode
{
// definition of node of binary tree
int data;
TreeNode *left;
TreeNode *right;
TreeNode(int data)
{
// constructor for generating binary tree node
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
// global variables for head pointer of
// doubly linked list
node *global_head = NULL;
node *temp = NULL;
void inorder(TreeNode *root)
{
// traversing inorder
if (root == NULL)
{
return;
}
inorder(root->left);
// creating a new node of doubly linked list
node *temp_head = new node(root->data);
// if there is no global head then the leftmost leaf node
// becomes head of doubly linked list
// else we continue to add new nodes to the linked list
if (global_head == NULL)
{
global_head = temp_head;
temp = global_head;
}
else
{
temp->next = temp_head;
temp_head->prev = temp;
temp = temp->next;
}
inorder(root->right);
}
int main()
{
// generating Binary Tree
TreeNode *root = new TreeNode(10);
root->left = new TreeNode(12);
root->right = new TreeNode(15);
root->left->left = new TreeNode(25);
root->left->right = new TreeNode(30);
root->right->left = new TreeNode(36);
inorder(root);
// displaying the linked list
while (global_head != NULL)
{
cout << global_head->data << " -> ";
global_head = global_head->next;
}
cout << endl;
return 0;
}
Output

Implementation in Java
class node {
// definition of the node of linked list
int data;
node next;
node prev;
node(int data) {
// constructor for generating linked list node
this.data = data;
this.next = null;
this.prev = null
}
}
class TreeNode {
// definition of the node of binary tree
int data;
TreeNode left;
TreeNode right;
TreeNode(int data) {
// constructor for generating node of binary tree
this.data = data;
this.left = null;
this.right = null;
}
}
class Main {
// global variables for head of doubly linked list
static node global_head = null;
static node temp = null;
public static void inorder(TreeNode root) {
// traversing inorder
if (root == null) {
return;
}
inorder(root.left);
// creates a node of doubly linked list
node temp_head = new node(root.data);
// if there is no global head then the leftmost leaf node
// becomes head of doubly linked list
// else we continue to add new nodes to the linked list
if (global_head == null) {
global_head = temp_head;
temp = temp_head;
} else {
temp.next = temp_head;
temp_head.prev = temp;
temp = temp.next;
}
inorder(root.right);
}
public static void main(String[] args) {
// generating Binary Tree
TreeNode root = new TreeNode(10);
root.left = new TreeNode(12);
root.right = new TreeNode(15);
root.left.left = new TreeNode(25);
root.left.right = new TreeNode(30);
root.right.left = new TreeNode(36);
inorder(root);
// displays the linked list
while (global_head != null) {
System.out.print(global_head.data + " -> ");
global_head = global_head.next;
}
System.out.println();
return;
}
}
Output

Complexity Analysis
Let's analyze the complexity analysis of the implementations above.
Time Complexity
As we are iterating over all the nodes of the tree, so our time complexity reaches O(n), where n is the number of nodes in the binary tree.
Space complexity
Let n be the number of nodes in the binary tree. So as we are generating a doubly linked list of size n, the space complexity reaches O(n).
Frequently Asked Questions
What is in-order Traversal? What is its time complexity?
Inorder Traversal in a tree is an algorithm to traverse all the tree nodes by following a specific pattern: left -> value -> right. We first visit the left child of a node, then we see the node, and then we call the right child of the node.
What types of traversals can we follow on a Binary Tree?
There are different types of traversals in a Binary Tree. Some are Inorder Traversal, Postorder Traversal, Preorder Traversal, and Breadth First Traversal. etc
What is a doubly linked list? How is it different from a singly linked list?
A doubly linked list is a linear data structure, where each node of the linked list is connected to the next and its previous node. Each node stores the data, next and prev.
What should be the time and space complexity of Insertion in a doubly linked list?
Insertion in the doubly linked list takes around O(n) time, as one has to iterate over the list to reach the end of the list, and then a new value is added.
Space complexity is O(1) for one node, as we create a new node for the attributes, so creating one node takes O(1) time.
What is the difference between Binary Tree and Binary Search Tree?
A Binary Search Tree, like Binary Tree, has two children, left and right. But the main difference arises in a Binary Search Tree; the left child is always smaller than the node's value, and the right child is always greater than the node's value.
Conclusion
So Ninjas!!, this blog discussed converting a binary tree to a doubly linked list using in-order Traversal. This helped you to get a better understanding of these topics.
This is a common interview question that assesses your understanding of two primary data structures (binary trees and linked lists) and your recursive and pointer (and reference) skills, so make sure you can create the code yourself.
Recommended Reading:
Check out The Interview guide for Product Based Companies and some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, Uber, Microsoft, etc. on Coding Ninjas Studio.
Also, check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, etc., as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.