Table of contents

Introduction

Algorithm

Code

Complexity analysis

FAQs

Key Takeaways

Last Updated: Mar 27, 2024

Deletion in Red-Black Trees

Author Malay Gain

Do you think IIT Guwahati certified course can help you in your career?

Yes

Introduction

Before discussing deletion in the Red-Black Tree, let’s revisit the properties of the Red-Black Tree. A red-black tree is one type of binary search tree that satisfies the following properties:

Every node is either red or black.
The root is black.
Every leaf (nil) is black.
If a parent node is red, then both of its children are black.
All simple paths from the node to descendant leaves contain the same number of black nodes for each node.

The deletion in the red-black tree is similar to the deletion operation in a binary search tree. But nodes have a colour property. After the deletion operation, we need to check all the properties of the red-black tree. If all the properties are not satisfied, we perform the following operation to make it a red-black tree.

Recolour
Rotation followed by recolouring.

Algorithm

The first step is to perform the process of deletion in BST. This step is the same as any BST. While performing this type of deletion, we always end up deleting a node that either has only one child or is a leaf. So we only need to handle cases where the node is a leaf node or has only one child. Let v be the node to be deleted, and u be the child that replaces v.

2. If either v or u is red, we mark the replaced child as black (deletion causes no change in black height). Note that as v is the parent of u, and two consecutive reds are not allowed in the red-black tree, both u and v cannot be red.

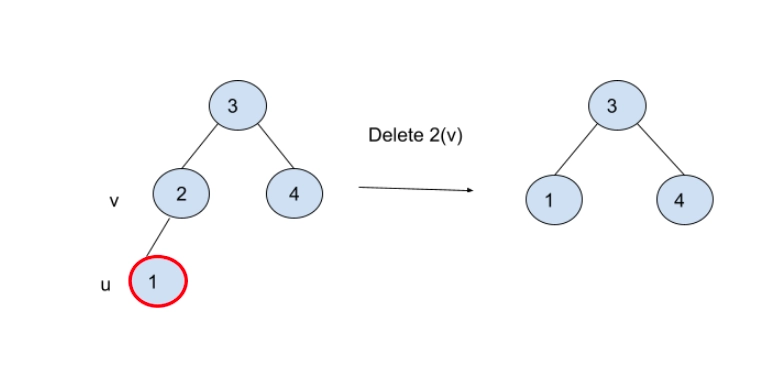
3. If Both u and v are Black

colour u as double black (keeping a node double-black, we know exactly where the black shortage is). Now the task reduces to convert this double black to single black. Note that If v is a leaf, then u is NULL, and the colour of NULL is considered black. So the deletion of a black leaf causes a double black.

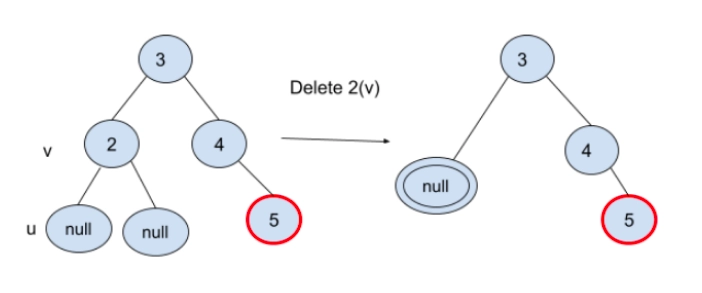
For a sibling node s of current node u that is double black but not the root

Case 1:

If sibling node s is black and at least one of its children is red, perform rotation for rebalancing the red-black tree. This case can be divided into four subcases depending upon positions of s and r, red child of s .

1. right-right( where s is the right child of its parent and r is the right child of s, or both children of s are red). See the below diagram for a better understanding.

2. right-left( where s is the right child of its parent and r is the red left child of s). See the below diagram for a better understanding.

3. left-left( where s is left child of its parent and r is left child of s; it is mirror case of the right-right case)

4. left-right(where s is left child of its parent and r is right child of s; it is mirror case of the left-right case)

Case 2:

If the sibling s is black and both of its children are black,

perform recolouring of nodes, and recur for the parent if the parent is

Black. See the below diagram for a better understanding.

Case 3:

If sibling s is red, perform a rotation to move the old sibling node up,

recolor the old sibling and parent. The new sibling is always black (See

the below diagram). This converts the tree to the black sibling case (by

rotation) and leads to previous cases. This case is divided into two

subcases; left and right cases.

1. right case(s is right child of its parent): left rotate the parent p to move the node up. See the below diagram for a better understanding.

2. left case ( s is left child of its parent): this mirror of the previous case. Here we perform the right rotation.

4. If u is the root, make it single black

Code

// algorithm for deletion in Red-Black Tree

rb_delete(t, z)
  if z->left = NULL or z->right = NULL
y ← z
  else y ← tree-successor(z)
  if y->left ≠ NULL
  x ← y->left
  else x ← y->right
  x->p ← y->p
  if y->p = NULL
  t->root ← x
  else if y = y->p->left
  y->p->left ← x
  else y->p->right ← x
  if y 3≠ z
  z->key ← y->key
  //copy y's satellite data into z
  if y->color = BLACK
rb_delete_fixup(t, x)
return y


rb_delete_fixup(t, x)
  while x ≠ t->root and x->color = BLACK
  do if x = x->p->left
  w ← x->p->right
  if w->color = RED
  w->color ← BLACK //Case 1
  x->p->color ← RED //Case 1
  left-rotate(t, x->p) //Case 1
  w ← x->p->right //Case 1
  if w->left->color = BLACK and w->right->color = BLACK
  w->color ← RED //Case 2
  x ← x->p //Case 2
  else if w->right->color = BLACK
  w->left->color ← BLACK   //Case 3
  w->color ← RED   //Case 3
right-rotate(t, w)   //Case 3
  w ← x->p->right   //Case 3
  w->color ← x->p->color //Case 4
  x->p->color ← BLACK //Case 4
  w->right->color ← BLACK //Case 4
  left-rotate(t, x->p) //Case 4
  x ← t->root /*Case 4*/
  else (same as then clause with "right" and "left" exchanged)
  x->color ← BLACK

Complexity analysis

In the worst case, the algorithm of deletion in the Red-Black Tree takes O(log N) time, where N is the number of nodes in the red-black tree and the worst-case space complexity O(N).

FAQs

1). What is the red-black tree?

A red-black tree is one type of binary search tree that satisfies the following properties:

Every node is either red or black.
The root is black.
Every leaf (nil) is black.
If a parent node is red, then both of its children are black.
All simple paths from the node to descendant leaves contain the same number of black nodes for each node.

2). What is the time complexity of deletion in Red-Black Tree?

It takes O(log N) time, where N is the number of nodes in the red-black tree.

3). What are the main operations performed while deletion of a node in Red-Black Tree?

Rotation and recolouring are the main operations performed while deletion in Red-Black Tree.

4). What is the application of a red-black tree?

It is used for implementing TreeSet, TreeMap in java and set, map in C++ STL library.

Key Takeaways

This article covered deletion in the Red-Black Trees. We have learned about the algorithm to delete a node in the Red-Black Tree and restore its property after deletion.

Side by side, we should also learn about insertion and searching operations in the Red-Black Tree.

Check out this problem - Largest BST In Binary Tree

Check out this problem - Root To Leaf Path

Apart from this, you can practice a wide range of coding questions commonly asked in interviews in Coding Ninjas Studio. Along with coding questions, we can also find the interview experience of scholars working in renowned product-based companies here.

Happy learning!