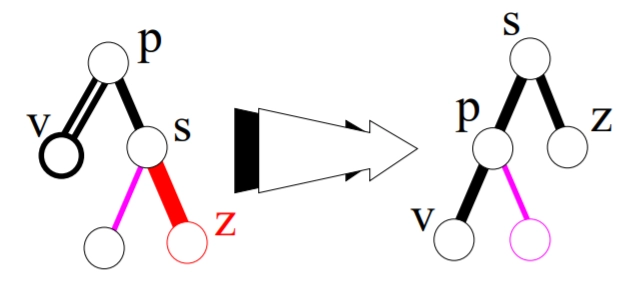
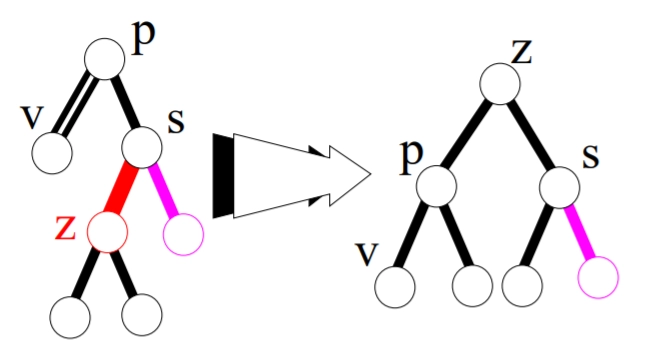
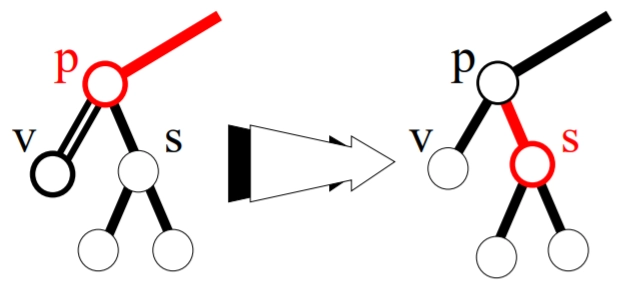
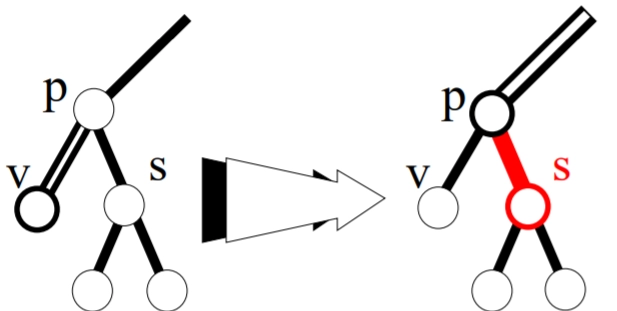
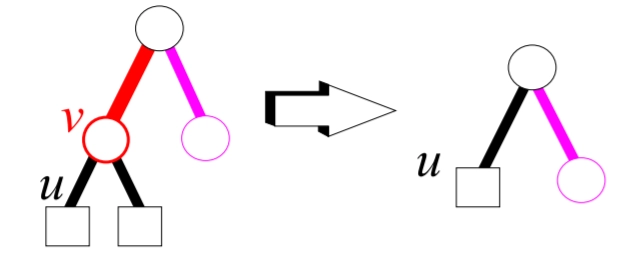Example
The following example illustrates the steps on how to delete a node in the Red-Black tree.

Both the children of 9 are black, so we introduce a double black node.
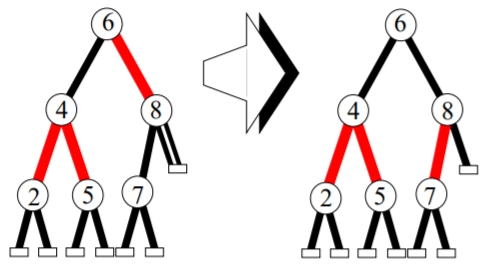
Since the parent of the double black node was red, we recolor both of them as black.
Now, delete 8 from the above tree. The left child of 8 is red, so we will simply replace 8 with 7 and color it black.

Now, delete 7 from the above tree. Both the children of 7 are black, so we introduce a double black node. The left sibling of 7 is black and has red children, therefore we perform the rotation operation of left left case.
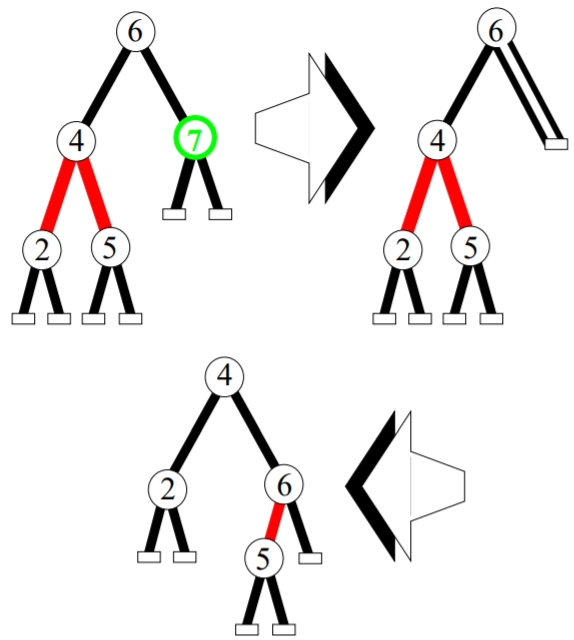
Source
C++ Implementation
#include <bits/stdc++.h>
using namespace std;
enum Color
{
RED,
BLACK,
DOUBLE_BLACK
};
struct Node
{
int data;
int color;
Node *left, *right, *parent;
explicit Node(int);
};
class RBTree
{
private:
Node *root;
protected:
void rotateLeft(Node *&);
void rotateRight(Node *&);
void fixInsertRBTree(Node *&);
void fixDeleteRBTree(Node *&);
void inorderBST(Node *&);
void preorderBST(Node *&);
int getColor(Node *&);
void setColor(Node *&, int);
Node *minValueNode(Node *&);
Node *maxValueNode(Node *&);
Node *insertBST(Node *&, Node *&);
Node *deleteBST(Node *&, int);
int getBlackHeight(Node *);
public:
RBTree();
void insertValue(int);
void deleteValue(int);
void merge(RBTree);
void inorder();
void preorder();
};
Node::Node(int data)
{
this->data = data;
color = RED;
left = right = parent = nullptr;
}
RBTree::RBTree()
{
root = nullptr;
}
int RBTree::getColor(Node *&node)
{
if (node == nullptr)
return BLACK;
return node->color;
}
void RBTree::setColor(Node *&node, int color)
{
if (node == nullptr)
return;
node->color = color;
}
Node *RBTree::insertBST(Node *&root, Node *&ptr)
{
if (root == nullptr)
return ptr;
if (ptr->data < root->data)
{
root->left = insertBST(root->left, ptr);
root->left->parent = root;
}
else if (ptr->data > root->data)
{
root->right = insertBST(root->right, ptr);
root->right->parent = root;
}
return root;
}
void RBTree::insertValue(int n)
{
Node *node = new Node(n);
root = insertBST(root, node);
fixInsertRBTree(node);
}
void RBTree::rotateLeft(Node *&ptr)
{
Node *right_child = ptr->right;
ptr->right = right_child->left;
if (ptr->right != nullptr)
ptr->right->parent = ptr;
right_child->parent = ptr->parent;
if (ptr->parent == nullptr)
root = right_child;
else if (ptr == ptr->parent->left)
ptr->parent->left = right_child;
else
ptr->parent->right = right_child;
right_child->left = ptr;
ptr->parent = right_child;
}
void RBTree::rotateRight(Node *&ptr)
{
Node *left_child = ptr->left;
ptr->left = left_child->right;
if (ptr->left != nullptr)
ptr->left->parent = ptr;
left_child->parent = ptr->parent;
if (ptr->parent == nullptr)
root = left_child;
else if (ptr == ptr->parent->left)
ptr->parent->left = left_child;
else
ptr->parent->right = left_child;
left_child->right = ptr;
ptr->parent = left_child;
}
void RBTree::fixInsertRBTree(Node *&ptr)
{
Node *parent = nullptr;
Node *grandparent = nullptr;
while (ptr != root && getColor(ptr) == RED && getColor(ptr->parent) == RED)
{
parent = ptr->parent;
grandparent = parent->parent;
if (parent == grandparent->left)
{
Node *uncle = grandparent->right;
if (getColor(uncle) == RED)
{
setColor(uncle, BLACK);
setColor(parent, BLACK);
setColor(grandparent, RED);
ptr = grandparent;
}
else
{
if (ptr == parent->right)
{
rotateLeft(parent);
ptr = parent;
parent = ptr->parent;
}
rotateRight(grandparent);
swap(parent->color, grandparent->color);
ptr = parent;
}
}
else
{
Node *uncle = grandparent->left;
if (getColor(uncle) == RED)
{
setColor(uncle, BLACK);
setColor(parent, BLACK);
setColor(grandparent, RED);
ptr = grandparent;
}
else
{
if (ptr == parent->left)
{
rotateRight(parent);
ptr = parent;
parent = ptr->parent;
}
rotateLeft(grandparent);
swap(parent->color, grandparent->color);
ptr = parent;
}
}
}
setColor(root, BLACK);
}
// Function to delete a node in the Red-Black tree
void RBTree::fixDeleteRBTree(Node *&node)
{
if (node == nullptr)
return;
if (node == root)
{
root = nullptr;
return;
}
if (getColor(node) == RED || getColor(node->left) == RED || getColor(node->right) == RED)
{
Node *child = node->left != nullptr ? node->left : node->right;
if (node == node->parent->left)
{
node->parent->left = child;
if (child != nullptr)
child->parent = node->parent;
setColor(child, BLACK);
delete (node);
}
else
{
node->parent->right = child;
if (child != nullptr)
child->parent = node->parent;
setColor(child, BLACK);
delete (node);
}
}
else
{
Node *sibling = nullptr;
Node *parent = nullptr;
Node *ptr = node;
setColor(ptr, DOUBLE_BLACK);
while (ptr != root && getColor(ptr) == DOUBLE_BLACK)
{
parent = ptr->parent;
if (ptr == parent->left)
{
sibling = parent->right;
if (getColor(sibling) == RED)
{
setColor(sibling, BLACK);
setColor(parent, RED);
rotateLeft(parent);
}
else
{
if (getColor(sibling->left) == BLACK && getColor(sibling->right) == BLACK)
{
setColor(sibling, RED);
if (getColor(parent) == RED)
setColor(parent, BLACK);
else
setColor(parent, DOUBLE_BLACK);
ptr = parent;
}
else
{
if (getColor(sibling->right) == BLACK)
{
setColor(sibling->left, BLACK);
setColor(sibling, RED);
rotateRight(sibling);
sibling = parent->right;
}
setColor(sibling, parent->color);
setColor(parent, BLACK);
setColor(sibling->right, BLACK);
rotateLeft(parent);
break;
}
}
}
else
{
sibling = parent->left;
if (getColor(sibling) == RED)
{
setColor(sibling, BLACK);
setColor(parent, RED);
rotateRight(parent);
}
else
{
if (getColor(sibling->left) == BLACK && getColor(sibling->right) == BLACK)
{
setColor(sibling, RED);
if (getColor(parent) == RED)
setColor(parent, BLACK);
else
setColor(parent, DOUBLE_BLACK);
ptr = parent;
}
else
{
if (getColor(sibling->left) == BLACK)
{
setColor(sibling->right, BLACK);
setColor(sibling, RED);
rotateLeft(sibling);
sibling = parent->left;
}
setColor(sibling, parent->color);
setColor(parent, BLACK);
setColor(sibling->left, BLACK);
rotateRight(parent);
break;
}
}
}
}
if (node == node->parent->left)
node->parent->left = nullptr;
else
node->parent->right = nullptr;
delete (node);
setColor(root, BLACK);
}
}
Node *RBTree::deleteBST(Node *&root, int data)
{
if (root == nullptr)
return root;
if (data < root->data)
return deleteBST(root->left, data);
if (data > root->data)
return deleteBST(root->right, data);
if (root->left == nullptr || root->right == nullptr)
return root;
Node *temp = minValueNode(root->right);
root->data = temp->data;
return deleteBST(root->right, temp->data);
}
// Function to delete a node in the Red-Black tree by value.
void RBTree::deleteValue(int data)
{
Node *node = deleteBST(root, data);
fixDeleteRBTree(node);
}
void RBTree::inorderBST(Node *&ptr)
{
if (ptr == nullptr)
return;
inorderBST(ptr->left);
cout << ptr->data << " " << ptr->color << endl;
inorderBST(ptr->right);
}
void RBTree::inorder()
{
inorderBST(root);
}
void RBTree::preorderBST(Node *&ptr)
{
if (ptr == nullptr)
return;
cout << ptr->data << " " << ptr->color << endl;
preorderBST(ptr->left);
preorderBST(ptr->right);
}
void RBTree::preorder()
{
preorderBST(root);
cout << "-------" << endl;
}
Node *RBTree::minValueNode(Node *&node)
{
Node *ptr = node;
while (ptr->left != nullptr)
ptr = ptr->left;
return ptr;
}
Node *RBTree::maxValueNode(Node *&node)
{
Node *ptr = node;
while (ptr->right != nullptr)
ptr = ptr->right;
return ptr;
}
int RBTree::getBlackHeight(Node *node)
{
int blackheight = 0;
while (node != nullptr)
{
if (getColor(node) == BLACK)
blackheight++;
node = node->left;
}
return blackheight;
}
// Test case 1 : 5 2 9 1 6 8 0 20 30 35 40 50 0
// Test case 2 : 3 0 5 0
// Test case 3 : 2 1 3 0 8 9 4 5 0
void RBTree::merge(RBTree rbTree2)
{
int temp;
Node *c, *temp_ptr;
Node *root1 = root;
Node *root2 = rbTree2.root;
int initialblackheight1 = getBlackHeight(root1);
int initialblackheight2 = getBlackHeight(root2);
if (initialblackheight1 > initialblackheight2)
{
c = maxValueNode(root1);
temp = c->data;
deleteValue(c->data);
root1 = root;
}
else if (initialblackheight2 > initialblackheight1)
{
c = minValueNode(root2);
temp = c->data;
rbTree2.deleteValue(c->data);
root2 = rbTree2.root;
}
else
{
c = minValueNode(root2);
temp = c->data;
rbTree2.deleteValue(c->data);
root2 = rbTree2.root;
if (initialblackheight1 != getBlackHeight(root2))
{
rbTree2.insertValue(c->data);
root2 = rbTree2.root;
c = maxValueNode(root1);
temp = c->data;
deleteValue(c->data);
root1 = root;
}
}
setColor(c, RED);
int finalblackheight1 = getBlackHeight(root1);
int finalblackheight2 = getBlackHeight(root2);
if (finalblackheight1 == finalblackheight2)
{
c->left = root1;
root1->parent = c;
c->right = root2;
root2->parent = c;
setColor(c, BLACK);
c->data = temp;
root = c;
}
else if (finalblackheight2 > finalblackheight1)
{
Node *ptr = root2;
while (finalblackheight1 != getBlackHeight(ptr))
{
temp_ptr = ptr;
ptr = ptr->left;
}
Node *ptr_parent;
if (ptr == nullptr)
ptr_parent = temp_ptr;
else
ptr_parent = ptr->parent;
c->left = root1;
if (root1 != nullptr)
root1->parent = c;
c->right = ptr;
if (ptr != nullptr)
ptr->parent = c;
ptr_parent->left = c;
c->parent = ptr_parent;
if (getColor(ptr_parent) == RED)
{
fixInsertRBTree(c);
}
else if (getColor(ptr) == RED)
{
fixInsertRBTree(ptr);
}
c->data = temp;
root = root2;
}
else
{
Node *ptr = root1;
while (finalblackheight2 != getBlackHeight(ptr))
{
ptr = ptr->right;
}
Node *ptr_parent = ptr->parent;
c->right = root2;
root2->parent = c;
c->left = ptr;
ptr->parent = c;
ptr_parent->right = c;
c->parent = ptr_parent;
if (getColor(ptr_parent) == RED)
{
fixInsertRBTree(c);
}
else if (getColor(ptr) == RED)
{
fixInsertRBTree(ptr);
}
c->data = temp;
root = root1;
}
return;
}
int main()
{
int data;
RBTree rbTree, rbTree2;
rbTree.insertValue(7);
rbTree.insertValue(3);
rbTree.insertValue(18);
rbTree.insertValue(10);
rbTree.insertValue(22);
rbTree.insertValue(8);
rbTree.insertValue(11);
rbTree.insertValue(26);
rbTree.insertValue(2);
rbTree.insertValue(6);
rbTree.insertValue(13);
rbTree.preorder();
rbTree.deleteValue(18);
rbTree.deleteValue(11);
rbTree.deleteValue(3);
rbTree.deleteValue(10);
rbTree.deleteValue(22);
rbTree.preorder();
return 0;
}

You can also try this code with Online C++ Compiler
Output
10 1
7 0
3 1
2 0
6 0
8 1
18 0
11 1
13 0
22 1
26 0
-------
13 1
7 0
6 1
2 0
8 1
26 1
-------
Time Complexity: O(logN)
Every path from the root to the leaf has same number of black nodes. When we delete a node in the Red-Black tree, either a double-black node is introduced or recoloring happens. Recoloring takes O(1) time. To remove a double-black node, we either rotate and recolor, which takes O(1) time or, propagate the double-black node upwards. Propagating the double black node will take O(height) time, and the height of the Red-Black tree is of order O(logN).
Therefore, the total time complexity to delete a node in the Red-Black tree is O(logN).
Space Complexity: O(1)
The deletion step searches for the required node and deletes it. To maintain the properties of the Red-Black tree, recoloring and rotations are used. These are implemented just by using a few variables. Therefore the space complexity of the approach is O(1).
FAQs
-
What is the Red-Black tree?
A Red-Black tree is a self-balancing Binary Search Tree having the following properties:
Every node has either a red or black color.
The root is always black.
No two red nodes can be adjacent.
Every path from the root to a leaf has the same number of black nodes.
-
What is the height of a Red-Black tree with N nodes?
A red-black tree with N nodes has height <= 2*log2(N+1).
Key Takeaways
We learned how to delete a node in the Red-Black tree. We discussed the rotations and recoloring operations that can be performed to maintain its properties. If you want to solve more such problems, you can visit Coding Ninjas Studio.
If you think that this blog helped you share it with your friends!. To be more confident in data structures and algorithms, try out our DS and Algo Course.
Check out this problem - Duplicate Subtree In Binary Tree
Until then, All the best for your future endeavours, and Keep Coding.