Introduction
Fractal geometry is a type of graphical depiction of mathematical functions or sets of numbers produced by mathematical functions. It is a recursive, comprehensive, and indefinitely self-similar mathematical system. "Unfolding Symmetry" can be seen in these geometrical renderings. The property of geometrical constructions to preserve a self-similar pattern at an infinitesimally small size is known as unfolding symmetry.
The Fibonacci Series is known to have a recursive relationship g(x) = g(x-1) + g(x-2) where x is the xth term in the series. Once again, g(0) = 0 and g(1) = 1.
Now let's see the approach to plot Fibonacci Spiral Fractal using Turtle in Python.
Approach to plot Fibonacci spiral Fractal
Each number in the plot Fibonacci spiral fractal is the series that represents the length of a square's sides. There is no such thing exist as a square with a side length of zero. As a result, we begin with a square with a side length of one. The next square has a side length of one as well.
- First, build two squares of dimensions, one side by side, as illustrated in the image below.
- Then, using the joint length of the two squares, we build a third square beneath the two squares of dimension 1. The square now has a dimension of 2.
- Using the two squares of dimensions 1 and 2, we construct the fourth square of dimension 3.
- Although we just went through a few iterations of this procedure, it continues indefinitely.
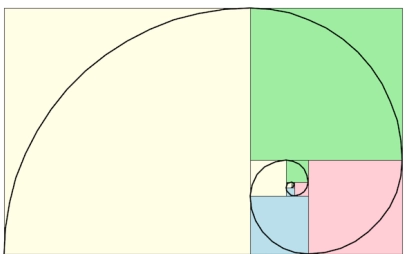
Plot Fibonacci Spiral Fractal using turtle
Source: https://pythonturtle.academy/fibonacci-spiral/
Now let's look at the code to plot Fibonacci Spiral Fractal using Turtle in Python.
You can also read about Palindrome Number in Python here.





