Introduction
Let's ensure we understand the foundational concepts before delving further into the subjects. Here is a brief introduction if you are unfamiliar with the Eigen.

The C++ template library Eigen is used for matrix and linear algebra operations. It supports all matrix sizes, including sparse matrices, small fixed-size matrices, and arbitrary huge dense matrices. We run our test suite against several compilers to ensure reliability and find any compiler bugs, and Eigen provides good support for these compilers.
In this blog, We will explain the details of SVD decomposition for real and complex matrices, with BDCSVD and jacobiSVD with their primary member function, constructor and destructor, and member function.
Without further ado, let's get started.
Understanding SVD decomposition
In this part, We talk about SVD decomposition for matrices (both real and complex). There are two decomposition algorithms offered:
🎯 JacobiSVD: For small matrices, two-sided Jacobi iterations are quickly implemented, but for bigger matrices, they take a very long time.
🎯 BDCSVD: Applying an upper-bidiagonalization that is still quick for large problems on top of a recursive divide-and-conquer approach.
💁 The corresponding classes and the following MatrixBase methods provide access to these decompositions:
- MatrixBase::jacobiSvd()
- MatrixBase::bdcSvd()
Class BDCSVD
Applying an upper-bidiagonalization that is still quick for large problems on top of a recursive divide-and-conquer approach.
template<typename MatrixType_, int Options_>
class Eigen::BDCSVD< MatrixType_, Options_ >
Template Parameters
☑️ Matrix Type_ which type of matrix are we using to compute the SVD decomposition
☑️ Options_ The options for computing unitaries U and V can be specified using this optional argument. ComputeFullV are examples of possible values. U or V cannot be ordered in both the thin and full versions. Unitaries are, by default, not computed.
This class divide-and-conquer diagonalizes the input matrix after first reducing it to bi-diagonal form using class UpperBidiagonalization. Class JacobiSVD is used to diagonalize small blocks. With the setSwitchSize() method, you can modify the switching size; the default is 16. As a result, it is preferable to apply JacobiSVD directly for small matrices (16). BDCSVD is strongly advised for larger ones and can be orders of magnitude faster.
Public Member Functions
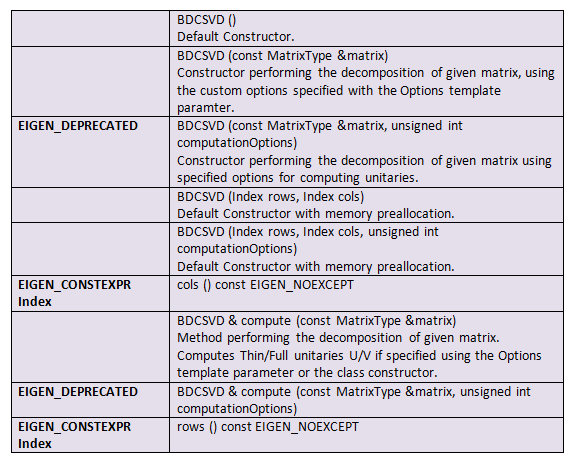
Constructor & Destructor
✅ BDCSVD() [1/5]
template<typename MatrixType_ , int Options_>
Eigen::BDCSVD< MatrixType_, Options_ >::BDCSVD ( )Default Constructor.
When using BDCSVD::compute to execute decompositions, the default function Object() { [native code] } can be handy (const MatrixType&).
✅ BDCSVD() [2/5]
template<typename MatrixType_ , int Options_>
Eigen::BDCSVD< MatrixType_, Options_ >::BDCSVD ( Index rows,
Index cols
)Preallocated memory in the default function Object() { [native code] }.
Similar to the default function Object() { [native code] }, but with internal data preallocated based on the problem size and Options template argument.
✅ BDCSVD() [3/5]
template<typename MatrixType_ , int Options_>
EIGEN_DEPRECATED Eigen::BDCSVD< MatrixType_, Options_ >::BDCSVD ( Index rows,
Index cols,
unsigned int computationOptions
)Memory preallocation in the default function Object() { [native code] }.
Similar to the default function Object() { [native code] }, but with internal data preallocated by the supplied problem size and computationOptions.
The function Object() { [native code] } and the Options template parameter cannot both be used to request unitiaries. Preferably use the Options template parameter.
✅ BDCSVD() [4/5]
template<typename MatrixType_ , int Options_>
Eigen::BDCSVD< MatrixType_, Options_ >::BDCSVD ( const MatrixType & matrix )Decomposition of the given matrix is carried out by the function Object() { [native code] } using the custom options specified in the Options template parameter.
✅ BDCSVD() [5/5]
template<typename MatrixType_ , int Options_>
EIGEN_DEPRECATED Eigen::BDCSVD< MatrixType_, Options_ >::BDCSVD ( const MatrixType & matrix,
unsigned int computationOptions
)Decomposes a given matrix using options for computing unitaries that are specified by the function Object() { [native code] }.
The function Object() { [native code] } and the Options template parameter cannot both be used to request unitiaries. Preferably use the Options template parameter.
Member Function Documentation
✅ cols()
template
EIGEN_CONSTEXPR Index Eigen::EigenBase< Derived >::cols ( void )return the number of columns.
✅ compute() [1/2]
template
BDCSVD& Eigen::BDCSVD< MatrixType_, Options_ >::compute (const MatrixType & matrix)a process for decomposing the given matrix. Calculate Thin/Full unitaries U/V if provided as a parameter in the Options template or in the class constructor.
✅ compute() [2/2]
template
EIGEN_DEPRECATED BDCSVD & Eigen::BDCSVD< MatrixType_, Options_ >::compute (const MatrixType & matrix, unsigned int computationOptions)According to the computationOptions parameter, a method is used to decompose the given matrix.
✅ rows()
template
EIGEN_CONSTEXPR Index Eigen::EigenBase< Derived >::rows (void )return the number of rows
Class JacobiSVD
Two-sided Jacobi iterations are quickly implemented for small matrices, but for bigger matrices, they take a very long time.
template<typename MatrixType_, int Options_>
class Eigen::JacobiSVD< MatrixType_, Options_ >
Template Parameters
🎯 Matrix Type_ which type of matrix are we using to compute the SVD decomposition
🎯 Options_ This optional parameter enables one to specify the kind of internal QR decomposition for the R-SVD step for non-square matrices. Additionally, one can choose to compute U and V in a thin or full unitary fashion. Look at the discussion of potential values below.
Any n-by-p matrix A is broken down using the SVD decomposition method as a product.
The singular values of A are denoted by the diagonal entries of S, while the left and right singular vectors of A are denoted by the columns of U and V, respectively. U is a real positive n-by-n unitary, V is a p-by-p unitary, and S is a real positive n-by-p matrix with a zero diagonal.
Singular values are always sorted in decreasing order.
By default, this JacobiSVD decomposition just computes the singular values. You must expressly request U or V if you want them.
This JacobiSVD class uses a two-sided Jacobi R-SVD decomposition for maximum accuracy and dependability. The drawback is that for large square matrices, it runs slower than bidiagonalizing SVD algorithms; nonetheless, its complexity is still O(n2p), i.e., the order of complexity is the same as the quicker bidiagonalizing R-SVD methods. R-SVD methods. Because its complexity is only linear in the larger dimension, it benefits from non-squareness, just like any R-SVD.
The algorithm is guaranteed to end in a limited (and sensible) amount of time, even if the input matrix has inf or nan coefficients, even though the outcome is undefined.
Public Member Functions
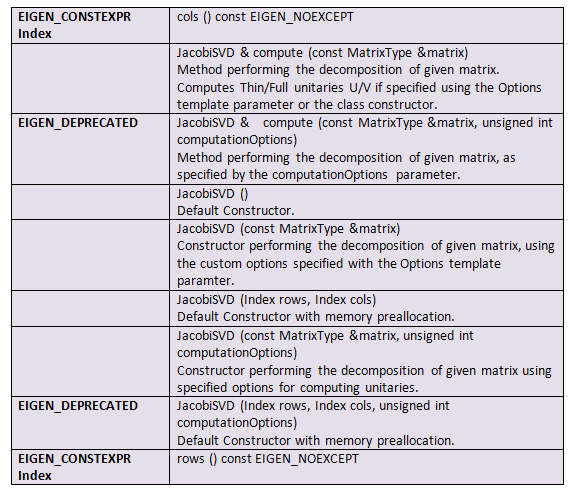
Constructor & Destructor
✅ JacobiSVD() [1/5]
template<typename MatrixType_ , int Options_>
Eigen::JacobiSVD< MatrixType_, Options_ >::JacobiSVD ( )Default Constructor.
When using JacobiSVD::compute to produce decompositions, the default function Object() { [native code] } can be handy (const MatrixType&).
✅ JacobiSVD() [2/5]
template<typename MatrixType_ , int Options_>
Eigen::JacobiSVD< MatrixType_, Options_ >::JacobiSVD (Index rows, Index cols ) Preallocated memory in the default function Object() { [native code] }.
Similar to the default function Object() { [native code] }, but with internal data preallocated based on the problem size and Options template argument.
✅ JacobiSVD() [3/5]
template<typename MatrixType_ , int Options_>
EIGEN_DEPRECATED Eigen::JacobiSVD< MatrixType_, Options_ >::JacobiSVD (Index rows, Index cols,
unsigned int computationOptions)Memory preallocation in the default function Object() { [native code] }.
Similar to the default function Object() { [native code] }, but with internal data preallocated by the supplied problem size and computationOptions.
The function Object() { [native code] } and the Options template parameter cannot both be used to request unitiaries. Preferably use the choice of the template parameter.
✅ JacobiSVD() [4/5]
template<typename MatrixType_ , int Options_>
Eigen::JacobiSVD< MatrixType_, Options_ >::JacobiSVD (const MatrixType & matrix )Decomposition of the given matrix is carried out by the function Object() { [native code] } using the custom options specified in the Options template parameter.
✅ JacobiSVD() [5/5]
template<typename MatrixType_ , int Options_>
Eigen::JacobiSVD< MatrixType_, Options_ >::JacobiSVD (const MatrixType & matrix, unsigned int computationOptions )Decomposes a given matrix using options for computing unitaries that are specified by the function Object() { [native code] }.
The function Object() { [native code] } and the Options template parameter cannot both be used to request unitiaries. Preferably use the Options template parameter.
Member Function Documentation
✅ cols()
template
EIGEN_CONSTEXPR Index Eigen::EigenBase< Derived >::cols ( void )return the number of columns.
✅ compute() [1/2]
template<typename MatrixType_ , int Options_>
JacobiSVD& Eigen::JacobiSVD< MatrixType_, Options_ >::compute ( const MatrixType & matrix )A process for decomposing the given matrix. If specified using the Options template parameter or the class constructor, compute Thin/Full unitaries U/V.
✅ compute() [2/2]
template<typename MatrixType_ , int Options_>
EIGEN_DEPRECATED JacobiSVD& Eigen::JacobiSVD< MatrixType_, Options_ >::compute ( const MatrixType & matrix, unsigned int computationOptions )\ According to the computationOptions parameter, a method is used to decompose the given matrix.
✅ rows()
template
EIGEN_CONSTEXPR Index Eigen::EigenBase< Derived >::rows (void )return the number of rows





