Introduction
We will begin our discussion with how to combine AdaBoost with decision trees and Random Forests because that is the most common way of using AdaBoost. So, if you are new to decision trees or Random Forests, check it out first. So let’s start by using decision trees and random forests for explaining the concepts behind AdaBoost.
In random forests, each time you make a tree, you make a full-sized tree.
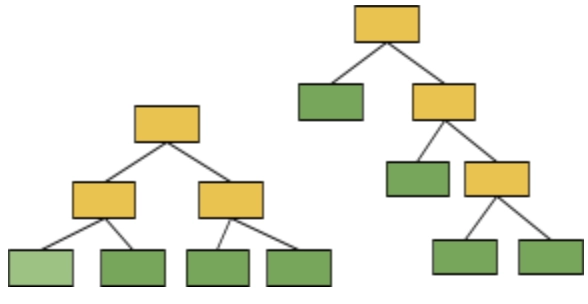
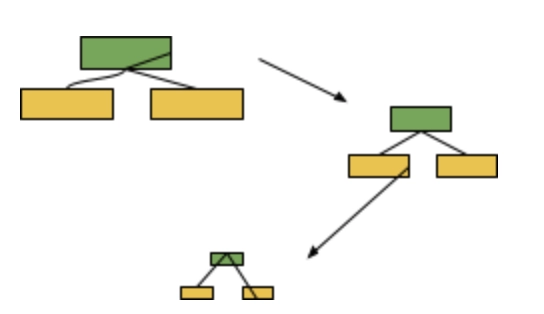
Some trees can be bigger than others, but there is no other predetermined maximum depth. The Forest of trees made with AdaBoost contains only one node and two leaves.
As you can see, the above figures have only one node and two leaves in them. A tree has one node and two leaves are called a stump. The above figure can better be described as a forest of stumps rather than trees. Stumps can’t make accurate classifications. For example, if we are using this data for determining if someone had heart disease or not.
| Chest pain | Good blood circulation | Blocked arteries | Weight | Heart disease |
| No | No | No | 125 | No |
| Yes | Yes | Yes | 180 | Yes |
| Yes | Yes | No | 210 | No |
| Yes | No | Yes | 167 | Yes |
A full-sized decision tree is responsible for taking advantage of all four variables that we measured(chest pain, good blood circulation, blocked arteries, weight, heart disease) for making a decision.
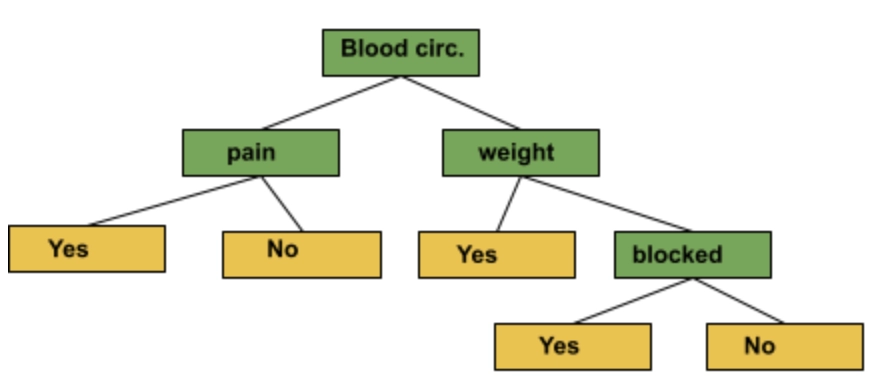
But, a stump uses only one variable for making a decision. Thus, stumps are technically “weak learners”. However, that’s the way AdaBoost likes it, and it’s one of the reasons why they are so commonly combined. Now, let’s come back to the random forest.
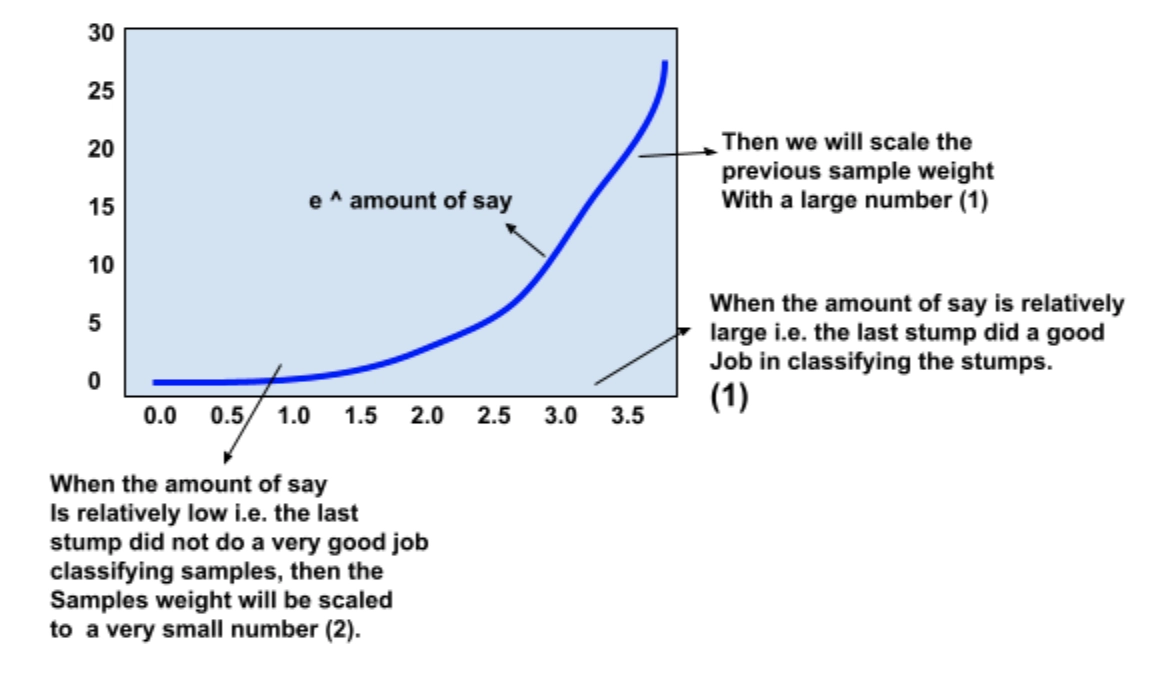
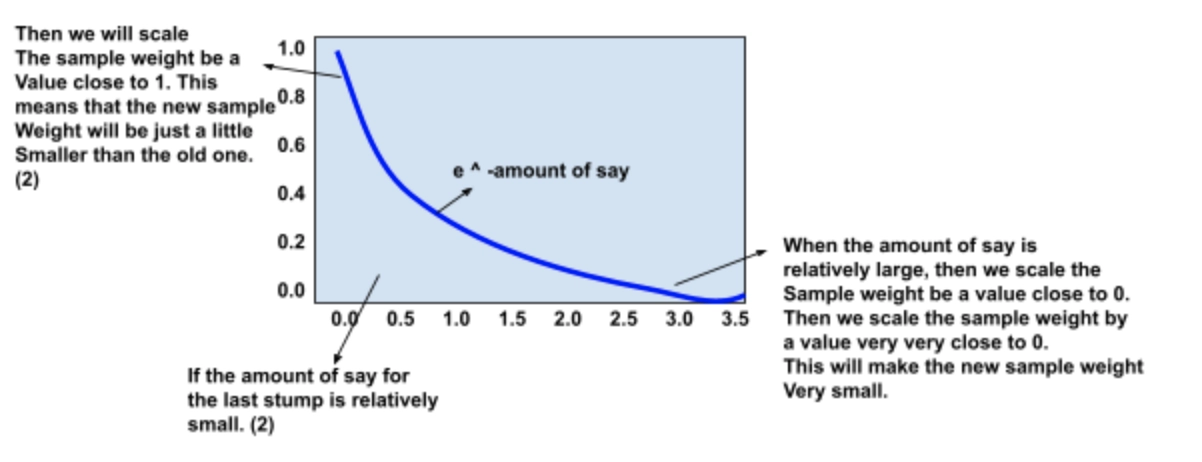
In a Random Forest, each tree provides an equal vote on the final classification. But in a forest of Stumps made with AdaBoost, some stumps get more say in the final classification than others.
In this illustration, the larger stumps get more say in the final classification than the smaller stumps.
Lastly, each decision tree in a Random Forest is made independently. In other words, 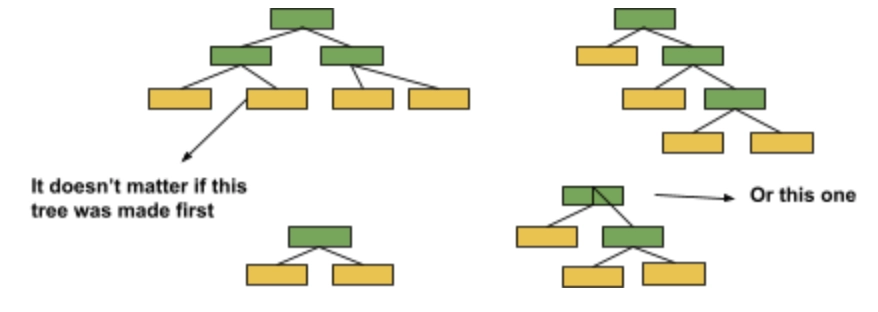
In contrast, in a Forest of Stumps made with AdaBoost, the order is important. The errors that the first stump makes influence how the second stump is made and the errors that the second stump makes influence how the third stump is made and so on.
The three ideas behind AdaBoost are:
- AdaBoost wraps a lot of “weak learners” to make classifications. The weak learners are always stumps.
- Some stumps get more say of proportion in the classification than others.
- Each stump is made by considering the previous stump’s mistake into account.
Now let’s dive into the nitty-gritty details of how to create a Forest of stumps using AdaBoost.
Creating Forests of Stumps: AdaBoost
First, let’s start with some data:
| Chest pain | Blocked arteries | Patient weight | Heart disease |
| yes | yes | 205 | yes |
| No | Yes | 180 | Yes |
| Yes | No | 210 | Yes |
| Yes | Yes | 167 | Yes |
| No | Yes | 156 | No |
| No | Yes | 125 | No |
| Yes | No | 168 | No |
| Yes | Yes | 172 | No |
Now, we will be creating a forest of stumps using AdaBoost for predicting whether any patient has heart disease. The decision will be based on the patient’s chest pain, blocked artery status, and weight. For that first give each sample a weight.
NOTE: the sample weight is different from the Patient’s weight. At the start, all samples will get the same weight that is 1Total number of samples.
| Sample weight |
| 1/8 |
| 1/8 |
| 1/8 |
| 1/8 |
| 1/8 |
| 1/8 |
| 1/8 |
| 1/8 |
In this case, 1total number of samples= ⅛. And, hence making all of them fairly important.
After the creation of the first stump, the weights will change for guiding us on how the next stump will be created. First of all, make the first stump of the forest. This is done by finding the variable that does the best job in the fields of chest pain, blocked arteries or patient weight. As all the sample weights are the same, we can ignore that. Let’s start by seeing how well Chest pain classifies the samples.
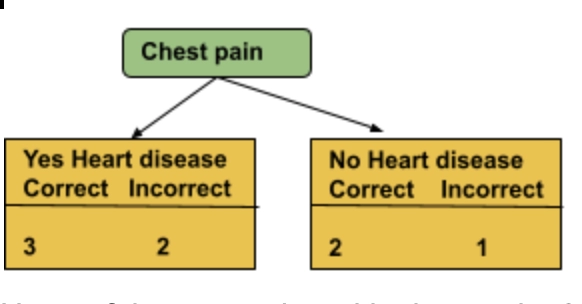
Here, of the 5 samples with chest pain, 3 were correctly classified as having a heart disease and 2 were incorrectly classified. Of the 3 samples without chest pain, 2 were correctly classified as not having heart disease and 1 was incorrectly classified. Now, for blocked arteries, we get:
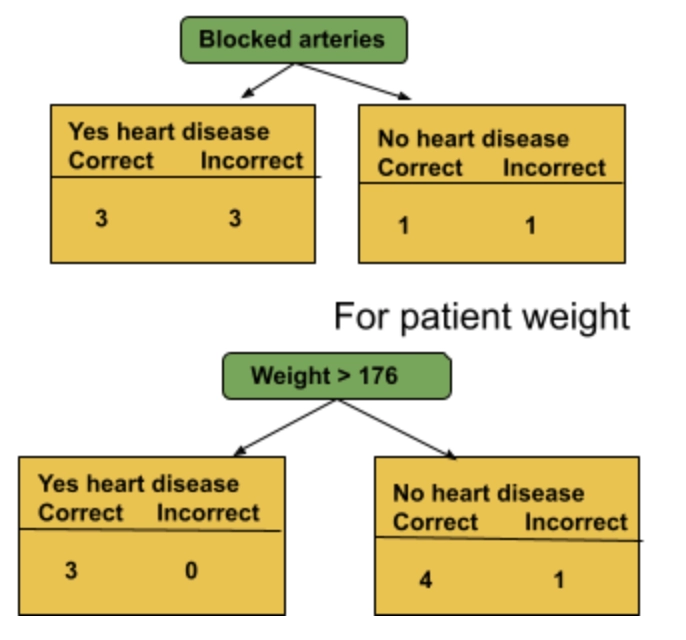
Now, we calculate the Gini Index for the three stumps. For chest pain, the Gini Index is 0.47, for blocked arteries: 0.55, and for weight: 0.2. We figure out that, the patient weight has the lowest Gini index and it will be our first stump. Now we need to determine how much say this stump will have in the final classification.
| Yes | Yes | 167 | Yes | 1/8 |
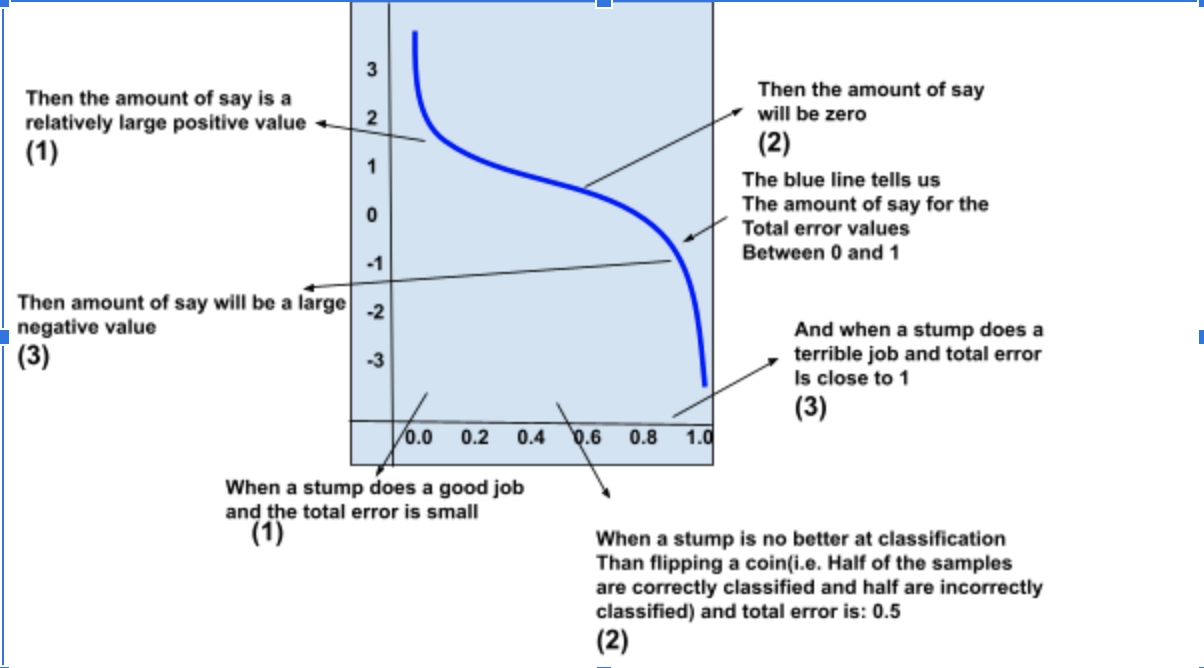
According to the stump, even if this patient weighs less than 176, they don’t have heart disease, which is incorrect. The total error is constituted with the sum of all weights related to the incorrectly classified samples. For this case, it is ⅛.
Note: Because all the sample weights add up to 1, the Total error will always be between 0, for a perfect stump and 1, for a horrible stump.